Le dessin technique

-- LE DESSIN TECHNIQUE en langage Java --
(appliquette)

--ooOoo--

- I - Introduction :

La présente rubrique traite des logiciels de dessins techniques. Elle expose ce qui me semble être indispensable pour qu'un tel logiciel soit en premier lieu au service de l'utilisateur, que ce dernier soit en permanence le maître de la situation ce qui suppose qu'il doit savoir où il va et ce qu'il doit faire. Le logiciel doit l'aider à faire son travail et aucunement à réfléchir ou à penser à sa place !..

Le but n'est pas de reproduire plus ou moins ce qui existe dans les logiciels existants que j'ai pu utiliser mais plutôt d'exposer une synthèse objective des outils de construction sur lesquels un logiciel de dessin, technique ou pas, devraient naturellement s'appuyer, à mon sens bien sûr, à la suite de quelques difficultés que j'ai rencontrées.

Pourquoi donc cette rubrique ?

Le modélisme fait partie de mes loisirs de bricolage. Donc pour réaliser une maquette en particulier, soit j'essaie de récupérer des plans sur la Toile soit je les réalise ou les adapte.

Sur la Toile on peut trouver facilement des plans de constructions documentés mais ils sont onéreux en général.
On peut y trouver tout aussi facilement des plans gratuits, mais ils sont souvent très succincts pour les exploiter directement. Le plan ci-dessous fourni sous la forme d'un fichier GIF, donne quelques indications de construction. Elles sont insuffisantes car les textes sont souvent petits et illisibles. Elles sont parfois dépourvues de notice de montage. C'est le revers de la gratuité. Personnellement, je donnerais tout ou ne donnerais rien. Le passage à la planche à dessin est donc obligatoire surtout si l'on souhaite changer l'échelle.

Comme j'essaie de réaliser quelques-unes de ces maquettes avec mon petit-fils, pour que cela ne soit pas trop lourd financièrement sans trop de conséquences avec la casse, le carton est le matériau privilégié. Par contre il est plus délicat à travailler que le bois et les pièces sont moins précises, généralement plus lourdes et là, le passage au dessin devient alors incontournable.

Jusqu'au système d'exploitation Windows Vista de Microsoft, j'utilisais un vieil outil de dessin ''Draft MicroCADAM'' distribué par ''Dassault Systèmes'' inspiré du logiciel de dessin industriel ''CADAM'' développé à l'origine par ''Lookheed''. Aux alentours des années 1995, j'avais pu l'obtenir du temps de mon activité dans la Société de construction d'hélicoptères dans le cadre de mon travail. Il remplissait parfaitement mes besoins.

Suite à une panne, je dus changer de PC. Sous Windows 7, ce vieux logiciel ne fonctionna plus et je me mis en quête d'un logiciel de dessin technique gratuit, bien entendu. C'est ainsi que je pus expérimenter les logiciels 2D vecteurs ci-après :

Ceux permettant de réaliser des dessins techniques, ceux qui permettent le positionnement numérique des entités les unes par rapport aux autres (parallèles, perpendiculaires, tangentes, etc...) :

''DraftSight'' du département ''Dassault Systèmes'' de la Société des ''Avions Marcel Dassault'' (beaucoup de ressemblances avec ''progeCAD Smart''),
''progeCAD Smart'' de la société ''progeSOFT IntelliCAD Technology'' (beaucoup de ressemblances avec ''DraftSight''),
''TurboCad 2D'',
''A9CAD'' de ''A9Tech'',
''QCad'' de ''RibbonSoft'',
''Draft IT '' de ''CADLogic''

Ceux ne permettant pas de réaliser des dessins techniques, ceux qui positionnent visuellement, donc sans précision, les entités les unes par rapport aux autres :

Il y en a beaucoup d'autres, mais voyant que les ergonomies étaient très proches les unes des autres, j'ai préféré arrêter.

Tous ces logiciels n'ont pas déclenché chez moi un grand enthousiasme tout en appréciant cependant leur existance :

l'intuitivité à laquelle j'attache beaucoup d'importance n'est pas au rendez-vous pour la plupart d'entre eux. Il faut chercher dans la documentation et même avec cette dernière, les procédures ne sont pas forcément évidente. Certes, on peut faire d'emblée des cercles, des droites de manière arbitraire et aléatoire mais quant à les positionner exactement en fonction de critères que l'on se donne, c'est une autre affaire.

l'ergonomie est la manière d'effectuer avec aisance les procédures dans le confort. Elle se retrouve sans originalité dans tous les logiciels comme s'il n'y avait qu'une manière de la concevoir. On peut s'y habituer certes mais sont-elles bien naturelles ?

Au final, après avoir repoussé périodiquement son installation, je me suis résolu à utiliser le système de virtualisation ''Oracle VM VirtualBox'', très bon produit, pour pouvoir installer un Windows XP afin de retrouver ainsi ce vieux logiciel MicroCADAM qui marche parfaitement et qui remplit la grande majorité de mes besoins. Pour parfaire parfois mes dessins, une sortie DXF permet une migration vers ''Inkscape'' (!!). L'image ci-dessous montre un dessin ''MicroCADAM'' sous Windows XP dans une fenêtre de VirtualBox :

A partir de mon expérience personnelle passée, je me suis donc posé un certain nombre de questions sur la manière de faire, la plus naturelle possible et la plus physiologique possible.

Tout au long de l'exposé, on raisonnera en 2D ce qui devrait pouvoir s'appliquer à chacun des 3 plans du 3D.

- II - Quelle est l'entité mathématique de base la plus fondamentale de toutes quelques soient les contextes ?

Il me semble que c'est le POINT.

Pourquoi ? car il est, dans la vie courante la référence incontournable de tous les jours pour indiquer un lieu ou une situation bien précise. Par exemple :

on se référera au ''point central'' d'une discussion, au ''point névralgique'', ''point sensible'' où les atteintes à l'intérêt d'un pays, à l'amour-propre d'un individu sont les plus sensibles,

on citera un ''rond point'' pour indiquer une direction,

on parlera ''d'un point de non retour'' si on ne peut revenir en arrière,

on dira qu'un plat est ''cuit à point'' d'une manière imagée dans le temps,

on pourra rappeler une manière toute aussi imagée d'employer le mot ''point'' dans les expressions que chacun d'entre nous a pu entendre ou dire au moins une fois, ''un point c'est tout !...'', ''.... point à la ligne !...'', ''... point barre !...'', etc... pour écourter une discussion par exemple.

Et là, je ne suis pas sûr que l'on puisse remplacer le mot point par le vocable d'une toute autre entité.

En informatique, il me paraît assez difficile de se passer du point, puisque pour voir toutes les informations sur un écran, une imprimante, le point est l'entité de base de toutes les codifications. Les ordinateurs ne peuvent se passer eux-même du ''bit'', un point en mémoire.

Mais alors, pourrait-on savoir pourquoi les développeurs modernes de logiciels de dessin technique ont-ils une aversion marquée envers le point pour ne pas le traiter de manière prioritairement explicite au lieu de l'utiliser un peu ''à la sauvette'' quand ils ont besoin de marquer une extrémité, un point milieu, un point de projection, une intersection, etc... ?

Dans tous ces logiciels, le point est considéré comme une entité de second ordre et je trouve quand même cela assez surprenant et dommage. Peut-être que le ''point'' est au graphique ce que le ''goto'' est au langage de programmation !!..

Comment devrait-on alors aborder l'entité point ?

Tout simplement, avec très grand soin, comme on le perçoit tout naturellement quand on fait un dessin à la main sur une feuille de papier ou une planche à dessin.

Remarque :

Le point est une entité qui n'est pas imprimée dans des documents diffusables. S'il doit l'être, il est marqué bien visiblement.

C'est la principale entité de construction géométrique.

Le logiciel doit mettre à disposition un outil de tracé de points spécifique, le plus élaboré possible dont une grande partie des cas ne se réduit qu'à l'affichage de ceux qui contribuent à la définition des entités donc sans aucun calcul.

Quelles sont donc les différentes situations où le point est un besoin incontournable ?

Légende des marquages dans les illustrations montrées en exemple :

		point positionné avec un clic de la souris, point existant sélecté ou point dont les coordonnées sont saisies au clavier,
		point calculé obtenu ,
		point milieu,
		point de sélection avec la souris,
		entité existante,
		entité calculée.

1 - Marquage d'une localisation de l'espace graphique par ses coordonnées.

Chaque point doit pouvoir être positionné :

soit par la souris, le positionnement est visuel donc approximatif aux attractions près,
soit par une saisie au clavier d'un point ou la modification des coordonnées du point sélecté suivant diverses techniques : dans des cadres sur la page, une fenêtre de propriétés ou une zone de commandes.

2 - Marquage en rapport avec une autre entité.

Sans anticiper sur la définition d'autres entités, on suppose ici qu'elles sont déjà dessinées. Chaque point doit pouvoir être placé comme suit :

A	:	la sélection de deux points (carré vert) permet d'obtenir le point milieu^(**).
B	:	la sélection d'un point et d'une droite permet d'obtenir la projection orthogonale du point sur la droite^(**).
C	:	la sélection d'un point et d'une ellipse permet d'obtenir la projection orthogonale du point sur cette ellipse à proximité du point de sélection car deux points répondent à la question^(**).
D	:	la sélection d'un point et d'une courbe (Béziers, Spline, B-Spline, etc...) permet d'obtenir la projection orthogonale du point sur la courbe à proximité du point de sélection car plusieurs points peuvent répondre à la question, dans certains cas il peut y en avoir aucun^(**).

(**) :

Dans l'appliquette, la fonction a été étendue en spécifiant par un mot-clé ''division'' le nombre de divisions à établir entre les deux entités indiquées.

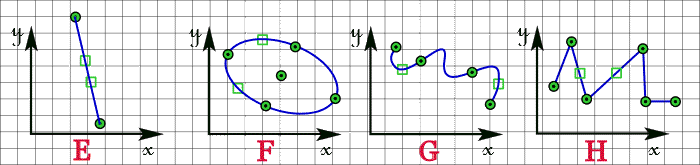
E	:	la double sélection d'une droite permet d'obtenir les points d'extrémité,
F	:	la double sélection d'une ellipse permet d'obtenir le centre et les extrémités des grand et petit axe,
G	:	la double sélection sélection d'une courbe permet d'obtenir les points de contrôle de la courbe,
H	:	la double sélection d'une ligne polygonale permet d'obtenir les extrémités et les sommets de la ligne polygonale,

Et d'une manière générale, la double sélection d'une entité permet d'obtenir les points de contrôle qui définissent l'entité et qui sont déjà en mémoire, sans nécessiter le moindre calcul.

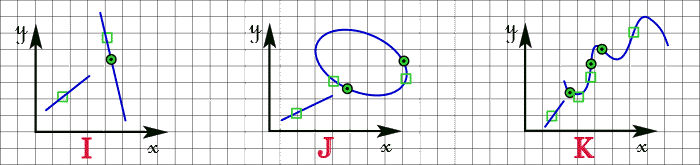
I	:	la sélection de deux droites permet d'obtenir le point d'intersection sauf si elle sont parallèles,
J	:	la sélection d'une droite et d'une ellipse permet d'obtenir, s'il existe, le point d'intersection le plus proche du point de sélection de l'ellipse,
K	:	la sélection d'une droite et d'une courbe permet d'obtenir, s'il existe, le point d'intersection le plus proche du point de sélection de la courbe,

Et d'une manière générale, la sélection d'une droite et d'une entité permet d'obtenir, s'il existe, le point d'intersection le plus proche du point de sélection de l'entité.

Remarque :

Les possibilités I, J, et K sont très importantes si le logiciel est seulement 2D car il permet de traiter des lignes de rappel dans des plans trois vues sans être obligé de prolonger les droites pour obtenir les intersections. C'est la raison pour laquelle le nom "droite" a été employé à la place de "segment (de droite)" pour laisser entendre leur caractère illimité .

dans ces cas, ces droites jouent pleinement le rôle
de droites de construction géométrique.

Exemple avec l'un de mes plans de maquette fait avec ''MicroCADAM'' :

L	:	la sélection de deux ellipses permet d'obtenir, s'il existe le point d'intersection le plus proche des deux points de sélection,
M	:	la sélection de deux courbes permet d'obtenir, s'il existe, le point d'intersection le plus proche des deux points de sélection,
N	:	la sélection d'une ellipse et d'une courbe permet d'obtenir, s'il existe, le point d'intersection le plus proche des deux points de sélection,

Tous les logiciels modernes que j'ai testés jusqu'à présent sont très loin de prendre en considération l'outil point comme il est présenté ici. Celui qui s'en approcherait le plus en en traitant en gros les ¾ serait peut-être le vieux logiciels "MicroCADAM".

- III - L'outil DROITE.

Partant de l'outil POINT décrit ci-dessus, l'outil droite s'en déduit tout naturellement puisqu'une droite est déterminée mathématiquement par 2 points.

On dessine une droite - à rappeler à caractère illimité - comme suit :

1 - Tracé d'une droite ou d'une ligne polygonale point à point

Ce tracé nécessite une fonction ''active/inactive'' pour différencier la droite simple d'une droite polygonale :

A	:	par la sélection de deux points (carré vert),
B	:	par la sélection d'un point et de l'une des extrémités d'une droite,
C	:	par la sélection de l'une des extrémités d'une droite et de l'une des extrémités d'une autre droite,
D	:	par la sélection d'un point ou de l'une des extrémités d'une droite et d'une autre droite : la droite obtenue est alors perpendiculaire à la droite sélectée, le point pouvant très bien se trouver sur la droite, dans ce cas une perpendiculaire est tracée de manière illimitée.

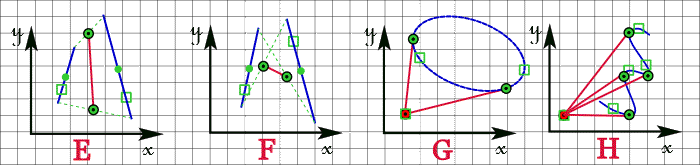
E et F	:	par la sélection de deux droites : la droite obtenue est celle qui joint les points milieu des extrémités deux à deux en fonction de la position relative des points de sélection^(**) :
		E -	la sélection porte sur les deux demi segments homologues, les points milieu sont ceux des extrémités homologues,
		F -	la sélection porte sur les deux demi segments croisés, les points milieu sont ceux des extrémités croisées,
G	:	par la sélection d'un point ou de l'extrémité d'une droite et d'une ellipse : la droite obtenue est la tangente qui joint le point sélecté au point de contact le plus proche du point de sélection de l'ellipse (2 solutions si le point sélecté est extérieur à l'ellipse),
H	:	par la sélection d'un point ou de l'extrémité d'une droite et d'une courbe (Béziers, Spline, B-Spline, etc..) : la droite obtenue est la tangente qui joint le point sélecté au point de contact le plus proche du point de sélection de la courbe (plusieurs solutions voire aucune),

I	:	par la sélection de deux ellipses : la droite obtenue est la tangente qui joint le point de contact le plus proche du point de sélection de la première ellipse au point de contact le plus proche du point de sélection de la seconde ellipse (2 ou 4 solutions si les deux ellipses sont extérieures l'une à l'autre),
J	:	par la sélection d'une ellipse et d'une courbe (Béziers, Spline, B-Spline, etc..) ou l'inverse : la droite obtenue est la tangente qui joint le point de contact le plus proche du point de sélection de l'ellipse au point de contact le plus proche du point de sélection de la courbe (plusieurs solutions),
K	:	par la sélection de deux courbes (Béziers, Spline, B-Spline, etc..) : la droite obtenue est la tangente qui joint le point de contact le plus proche du point de sélection de la première courbe au point de contact le plus proche du point de sélection de la seconde (plusieurs solutions),

2 - Tracé d'une droite verticale ou horizontale

Ce tracé nécessite une fonction ''active/inactive'' pour différencier le choix ''droite verticale''/''droite horizontale'' :

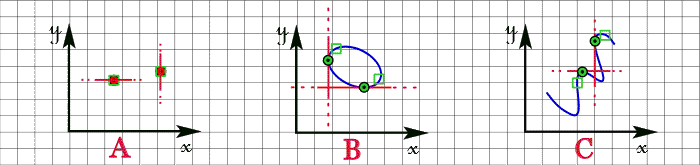
A	:	par la sélection, la numérisation ou la saisie des coordonnées d'un point,,
B	:	par la sélection d'une ellipse : la droite verticale ou horizontale illimitée obtenue passe par le point de contact le plus proche du point de sélection,
C	:	par la sélection d'une courbe : la droite verticale ou horizontale illimitée obtenue passe par le point de contact le plus proche du point de sélection,

3 - Tracé d'une droite normale à une entité

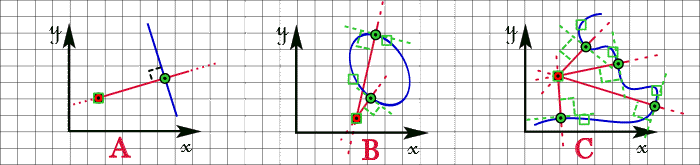
A	:	par la sélection, la numérisation ou la saisie des coordonnées d'un point suivie de la sélection d'une droite : la normale passe par le point,
B	:	par la sélection, la numérisation ou la saisie des coordonnées d'un point suivie de la sélection d'une ellipse : la normale illimitée obtenue passe par le point de contact le plus proche du point de sélection (2 solutions voire confondues),
C	:	par la sélection, la numérisation ou la saisie des coordonnées d'un point suivie de la sélection d'une courbe : la normale illimitée obtenue passe par le point de contact le plus proche du point de sélection (plusieurs solutions),

4 - Tracé d'une droite parallèle à une entité

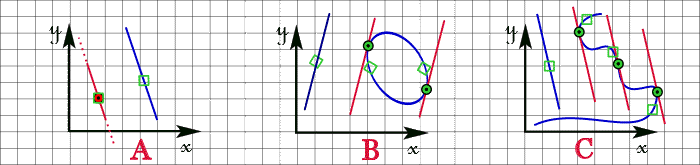
A	:	par la sélection, la numérisation ou la saisie des coordonnées d'un point suivie de la sélection d'une droite : la parallèle passe par le point,
B	:	par la sélection d'une ellipse suivie de la sélection d'une droite : la parallèle illimitée obtenue est tangente au point de contact le plus proche du point de sélection de l'ellipse (2 solutions voire confondues),
C	:	par la sélection d'une courbe suivie de la sélection d'une droite : la parallèle illimitée obtenue est tangente au point de contact le plus proche du point de sélection (plusieurs solutions),

5 - Tracé d'une droite formant un angle avec l'horizontale

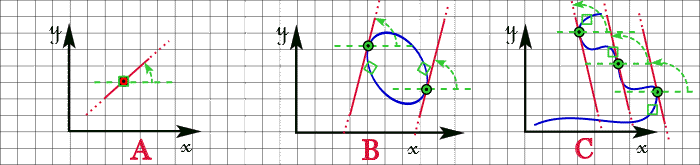
A	:	par la sélection, la numérisation ou la saisie des coordonnées d'un point suivie de la saisie de l'angle au clavier : la droite illimitée passe par le point,
B	:	par la sélection d'une ellipse suivie de la saisie de l'angle au clavier : la droite illimitée obtenue est tangente au point de contact le plus proche du point de sélection de l'ellipse (2 solutions voire confondues),
C	:	par la sélection d'une courbe suivie de la saisie de l'angle au clavier : la droite illimitée obtenue est tangente au point de contact le plus proche du point de sélection (plusieurs solutions),

- IV - L'outil ELLIPSE/CERCLE

Ici l'outil ELLIPSE sera limité car il pose quelques problèmes de détermination et de traitements analytiques. Une ellipse sera définie par un choix entre les trois fonctions suivantes :

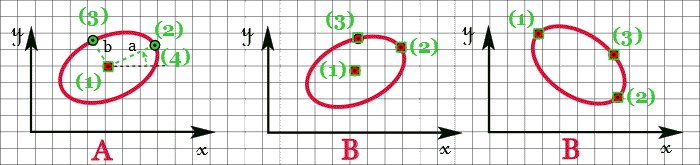
A	:	par la sélection, la numérisation ou la saisie des coordonnées du centre de l'ellipse, par la saisie au clavier de la longueur du demi-grand axe ''a'', de la longueur du demi-petit axe ''b'' et de l'angle de rotation,
B	:	par la sélection, la numérisation ou la saisie des coordonnées du centre de l'ellipse, de l'une des extrémités du grand axe et des coordonnées d'un point,
C	:	par la sélection, la numérisation ou la saisie des coordonnées d'une extrémité du grand diamètre, de l'autre extrémité du grand diamètre et d'un point.

Par contre, l'outil CERCLE sera plus riche et sera défini par un choix entre les fonctions suivantes :

A	:	par la sélection, la numérisation ou la saisie des coordonnées du centre du cercle et par la saisie au clavier de la longueur du rayon,
B	:	par la sélection, la numérisation ou la saisie des coordonnées du centre du cercle et d'un point,
C	:	par la sélection, la numérisation ou la saisie des coordonnées de deux points formant un diamètre.

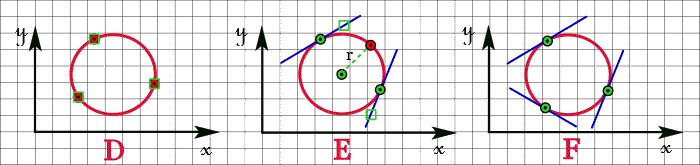
D	:	par la sélection, la numérisation ou la saisie des coordonnées de trois points,
E	:	par la sélection de deux tangentes et d'un point ou par la saisie au clavier de la longueur du rayon,
F	:	par la sélection de trois tangentes.

Remarque :

L'outil ARC d'ellipse ou de cercle n'a pas besoin, à mon sens bien sûr, d'être traité spécifiquement car, sitôt que l'ellipse ou le cercle est défini, une fonction ''coupure'' (break) suivie de deux fonctions ''relimitations'' (relim) définit parfaitement un ''arc''. Par ailleurs, la fonction ''filet'' (filet), bien utile en dessin technique, assure aussi le dessin d'un arc de cercle. Personnellement, je n'utilise que très peu l'outil ''arc'' proposé dans les logiciels.

- V - L'outil COURBE

L'outil COURBE consiste à définir une courbe par points de type Béziers, Spline ou B-Spline comme suit :

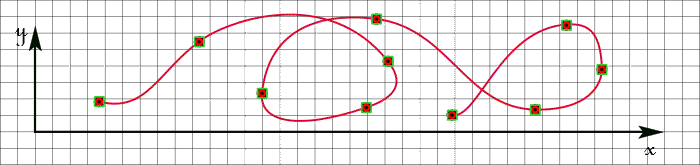
par la sélection, la numérisation ou la saisie des coordonnées des ''n'' points de contrôle de la courbe,

- VI - L'outil MODIFICATION

     Le but de cette rubrique n'est pas de décrire en détail l'outil MODIFICATION mais plutôt de faire quelques remarques. Cet outil est d'une importance capitale. Il permet de juger la qualité d'un logiciel quant à sa puissance donc à ses possibilités.

     Mais ce n'est pas tout !

     La qualité d'un logiciel se mesure aussi à travers l'intuitivité des opérations à effectuer. Ce vocable entraîne automatiquement la facilité et le confort qu'a l'utilisateur à se servir de son logiciel. En effet, si l'utilisateur n'est pas en mesure de deviner la plupart du temps les marches à suivre, si le guidage en parallèle est ténébreux ou incomplet, s'il doit en permanence avoir recours à la documentation même après une formation importante et onéreuse et s'il doit se ''reformer'' après être resté 2 ou 3 semaines sans l'utiliser, on peut se poser des questions sur la qualité de ce logiciel même s'il est super puissant mathématiquement.

     Mais il ne faut pas perdre néanmoins de vue que, pour tout logiciel, un apprentissage minimum est incontournable. Cependant, la période d'adaptation devrait être la plus courte possible et varie bien naturellement en fonction de la richesse de ses fonctionnalités.

Comment devrait se faire le choix entre plusieurs options ?

Dans la majorité des logiciels que j'ai utilisés, cette situation se présente quand on veut dessiner une entité comme une droite, par exemple. Dès que la souris passe à proximité d'un point caractéristique, sans qu'on le lui demande (^-1-), le logiciel propose un point (snap) ''quadrant'', un ''centre'', une ''extrémité'', une ''tangente'', etc... La procédure paraît très séduisante au demeurant. Eh bien, c'est le cas typique où l'utilisateur n'est pas le maître de la situation. Pourquoi ? il m'est arrivé plusieurs fois d'avoir à choisir un point parmi des points caractéristiques très proches. Le logiciel choisissait la plupart du temps le point qui ne m'intéressait pas après un tâtonnement un peu désagréable avec la souris. Pour y remédier, j'étais contraint de passer à grande échelle.

Il me semble qu'un choix explicite, ''tangente'', ''horizontale'', ''verticale'', etc... est préférable. L'utilisateur est censé savoir parfaitement ce qu'il fait pour contrôler la procédure. Le logiciel sert à l'aider et non à penser à sa place.

(^-1-)

Dans la programmation de la souris, bien que ce soit la mode (!), l'option ''MouseOver'' que personnellement je n'utilise pratiquement pas, est généralement un mauvais choix, même conceptuel.

Pourquoi ?

Justement parce que le programme prend délibérément l'ascendant sur l'utilisateur en proposant des solutions qui, quand elles sont très proches, génère une instabilité visuelle très désagréable sans lui rendre service, c'est même parfois une vraie calamité. Pour s'en convaincre, il suffit tout simplement de naviguer dans les menus déroulants en cascade d'Internet Explorer ou FireFox pour voir apparaître ceux que l'utilisateur ne veut pas en l'obligeant à faire des retours en arrière car la souris n'est pas restée rigoureusement sur la ligne adéquate. Plus grave encore, sous l'explorateur Windows, je ne compte plus les fois où j'ai déplacé des dossiers ou des fichiers sans le vouloir.

Par contre, l'option ''OnClick'' est autrement préférable. La souris pourra être promenée partout sans aucune réaction du programme qui, dans ce cas, attendra patiemment un clic volontaire de l'utilisateur pour réagir. Le programme reste à son service.

Par ailleurs, on pourrait s'intéresser à l'impact sur le taux d'occupation de l'unité centrale qu'engendre une action de type ''MouseOver'', surtout quand le déplacement d'une image ou d'une fenêtre y est asservi. L'interface surveille en permanence (polling) la position du pointeur et recalcule à chaque fois l'image ou la fenêtre alors qu'une action ''OnClick'' initialise l'interruption sur évènement souris, se met en sommeil (wait) qu'un click réveillera pour le traitement. Une mise en pause n'est presque pas consommatrice de CPU. Je dis presque car, en réalité pendant la pause, l'interface permet à l'utilisateur de bouger sa souris comme il l'entend sans aucune réactivité.

Comment devrait s'effectuer l'enchaînement des fonctions successives ?

Il est assez fréquent qu'une fonction soit utilisées plusieurs fois de suite, l'une après l'autre. Pourquoi donc la majorité des logiciels demandent-ils explicitement de répéter le choix effectué ?

Il me semble plus logique que le logiciel boucle sur la dernière fonction choisie tant qu'une autre fonction n'a pas été demandée.

Comment devrait s'effectuer le traitement d'une fonction ?

     Dans la plus grande généralité possible. Par exemple, la majorité des logiciels traitent la fonction ''échelle'' (scale) avec un facteur unique. Or il y a 2 coordonnées si le dessin est en 2D, 3 en 3D. Il devrait donc prendre en compte un facteur d'échelle spécifique à chaque coordonnées.

     Bien sûr, les logiciels sont capables de réaliser la fonction, souvent en passant par la fonction ''bloc'' qui n'est pas des plus pratiques pour cela et qui semble quand même être faite pour d'autres usages.

     Il serait souhaitable par ailleurs qu'il y ait séparation entre la définition mathématique d'une entité et ses attributs.

     Par exemple : je suis un utilisateur régulier du logiciel ''Inkscape''. Je trouve assez désagréable et ennuyeux aussi que les dimensions d'une entité, modifiables par une saisie au clavier, dépendent de l'épaisseur des traits, attribut qui n'intervient nullement dans sa définition mathématique. On a quelques difficultés à opérer des corrections dans les unités du dessin.

     J'ai d'ailleurs envoyé deux messages et une proposition (blueprint) à l'équipe ''Inkscape'' pour évoquer la possibilité de positionner mathématiquement les entités graphiques dans la perspective de créer des dessins techniques :

En français :	https://answers.launchpad.net/inkscape/+question/182376 (19-12-2011)
En anglais :	https://answers.launchpad.net/inkscape/+question/182449 (20-12-2011)
Proposition :	https://blueprints.launchpad.net/inkscape/+spec/technical-drawings-inkscape (cette page) (9-01-2012)

J'ai tout mon temps et n'ai aucun délai : et si j'essayais d'illustrer le propos ?.... juste pour voir et m'amuser : gros ''machin'' tout de même !...

     Dans tout ce qui précède, je me suis contenté de formuler une vision personnelle du traitement des entités graphiques dans laquelle il est très facile d'émettre des propositions : ''il faudrait que...'', "il n'y a qu'à ...'', "il faut qu'on...''. Mais sont-elles réalistes et quelle énergie de programmation faudrait-il déployer pour les satisfaire ?

     N'ayant, par ailleurs, rien trouvé d'analogue fonctionnant dans une page Web mais plutôt des logiciels à télécharger, je me suis donc fixé l'objectif de réaliser un programme pour illustrer cette vision en pensant qu'une appliquette Java ferait très bien l'affaire : elle ne dépend pas d'un système d'exploitation comme l'est un CGI écrit en C. Par ailleurs aussi, l'intérêt a résidé dans le fait que je ne connaissais pas le langage Java et qu'il m'a permis de l'apprendre un petit peu. A l'âge de 71 ans passé, la programmation que je pratique depuis le début de mes études en facultés est un passe-temps agréable et, qui sait ?... me permet de lutter contre Elzheimer en espérant ne pas terminer trop ''idiot'' !!!!.....

     E puèi Zou !.... finfinalo... (en provençal)... je le fais aussi dans l'espoir qu'il servira un peu à mon petit-fils et ma petite-fille pour leur initiation au dessin assité par ordinateur, pour leur travail en mathématique et en géométrie descriptive.

     Après les quelques essais traditionnels avec l'aide de quelques documentations livresques et, surtout, d'explications dans les tutoriels universitaires et ceux de différents forums - grand merci à tous -, je me suis donc lancé dans l'écriture de cette petite(!) appliquette graphique que j'ai voulue sobre et interactive bien entendu. Bien que je ne sois pas un mathématicien émérite, la partie mathématique, réduite aux points, aux droites et aux cercles, est élémentaire et assez légère ce qui n'est pas le cas de l'interface-utilisateur plus lourde, du reste sans grande complexité, comme le sont toutes les interfaces interactives car la programmation est assez mécanique.

     Cette expérience ne restaure pas le travail si l'on réactive la page HTML et elle ne prend pas en compte la sauvegarde du ''travail''. Il aurait fallu pour cela entrer dans le jeu d'approbation de certificat pour permettre l'écriture de fichiers sur l'ordinateur-client. Ce n'était pas le sujet....

     .... mais, vu les performances grandissantes du réseau Internet, cela pourrait être un appel du pied à des équipes spécialisées, beaucoup plus compétentes que moi, pour proposer un éditeur sérieux de dessin technique en ligne, donc continuellement à jour, gratuit bien sûr, qui pourrait grandement servir nos jeunes collégiens, en leur épargnant de lourds téléchargements et installations.

     Voici donc, une petite présentation de cette appliquette et commençons par une description schématique de l'espace de travail :

     La figure ci-dessus montre les différents espaces pris en compte sur celui de l'appliquette. En noir, ces surfaces sont utilisés pour l'affichage des menus , des invites et des informations ainsi qu'une zone d'écho des saisies-clavier. La surface BCDE en couleur dégradée est la fenêtre de visualisation des entités graphiques créées dans le système d'axes S en tenant compte du facteur de zoom.

     On sera probablement surpris par la tonalité sombre de l'ensemble. J'aime bien cela car les dessins de détachent bien visibles sur l'écran et que, par ailleurs, c'est une manière de protéger l'écran puisque les couleurs sombres émettent peu de lumière donc peu de courant dans les cellules.

     Enfin, je n'utilise dans cette appliquette que les événements de la souris (coordonnées et boutons) et ceux du clavier pour entrer du texte et des nombres. L'utilisation de boutons, de cases à cocher multiples ou exclusives de menus déroulants, etc... ne simplifie pas forcément la programmation et entraîne une manipulation d'images inutiles ici et inévitablement plus lourdes à télécharger ou à générer ce qui prend plus de temps contrairement à l'affichage des options indiquées par des mots-clé texte. Il est néanmoins possible de manipuler et de traiter des images puisque l'espace de base est une matrice de points (pixelmap) : exemples, le fond dégradé et le logo affiché dans le coin supérieur gauche de l'appliquette. L'interface ne peut pas être plus sobre pour une esthétique, pour moi, largement suffisante et toute aussi efficace.

     L'expérience vaut peut-être la peine d'être tentée. Vu ma faible expérience dans ce langage, le source n'est certainement pas un modèle du genre. Sans trop savoir si je suis bien dans la philosophie de Java, j'aborde le sujet, grosso-modo suivant le même découpage, comme si j'avais à le traiter en C avec lequel Java a beaucoup de points communs.

     Une remarque cependant :

      En 35 années d'informatique, j'ai maintes fois formulée cette remarque sur un aspect particulier très répandu du graphique en général proposé dans la majorité des librairies de base livrées par les fournisseurs :

L'origine de l'espace graphique primaire est presque toujours positionné sur le coin supérieur gauche
entraînant du même coup l'orientation de l'axe des ordonnées vers le bas !...

     C'est un choix non-conventionnel et, s'il ne présente aucune difficulté mathématique et semble en apparence très anodin, il génère tout de même des nuisances inutiles non négligeables.

     Du temps des premiers traceurs de courbes, au début des années 1960, la norme était respectée. Cette particularité est apparue avec les terminaux graphiques à mémoire. Ce choix avait été guidé au départ par l'implantation en mémoire de l'espace graphique sous forme de matrice de bits puis matrice de points par la suite, l'origine étant repérée par l'adresse du début de cette matrice.

     Or, si l'on regarde tous les logiciels graphiques proposés sur le marché depuis de longues années, l'origine des axes reste conventionnelle. Cela veut dire que les développeurs de chaque logiciel ont systématiquement réalisé la transformation du système d'axes.

     Je trouve fort surprenant qu'aujourd'hui encore cette particularité perdure dans des librairies modernes comme celle de Java. Il est tellement plus simple de la prendre en compte à la source.

    Je me suis donc toujours interrogé sur le souci de qualité de service des équipes relativement restreintes de développement d'origine qui, en proposant ce choix hors norme, ont généré et génèrent toujours des nuisances, (on s'y fait certes... la preuve !..), à une foule de développeurs des milliers de fois plus nombreux.

L'appliquette est réduite à sa plus simple expression. Elle est présentée au fur et à mesure de l'avancement de son écriture. Son fonctionnement, décrit dans la page ''description'', est centré sur :

la souris dont on a utilise uniquement les coordonnées dans l'espace de l'appliquette et seulement 2 boutons pour les souris les moins avancées où :

le bouton gauche a une fonction d'indication des options dans les menus et d'indication de points dans l'espace graphique,
le bouton droit sert à valider une option ou une opération si nécessaire.

la clavier qui permet de saisir des valeurs numériques et des textes. L'édition de la saisie (traitement des caractères spéciaux) n'a pas été développée mais ne pose pas de problème particulier.

L'interface interactive s'efforce de donner une marche à suivre par des messages d'invite dont l'objectif et de proposer un dialogue le plus intuitif possible, avec l'idéal caché de fournir des procédures naturelles sans recours important à la documentation, sinon, .... c'est complètement loupé !... Mais je compte sur mes deux très jeunes petits-enfants pour me mettre à l'épreuve.

La couleur marron a été choisie pour marquer les entités sélectées lors d'opérations multiples mais peut quand même étre utilisée comme toute autre couleur.

Enfin, désolé pour les bogues qui existent forcément encore.
Cependant, je ne pense pas continuer son développement car, finalement, le principe même de l'appliquette est une mauvaise solution. Et pour cause, à ma connaissance, personne jusqu'ici n'a tenté de faire un éditeur conséquent sous cette forme.

De plus, le plug-in JAVA qui supporte les applets a été abandonné dans les navigateur web "Mozilla FireFox", "Google Chrome" et "Microsoft Edge". Elle fonctionne cependant sous "Internet exploreur" et peut-être sous d'autres comme "Safari" par exemple..

Pour résumer la description développée ICI, au risque de paraître prétentieux !... je dirai que le principe de l'appliquette est fort intéressant à la base, sans nul doute, mais que sa prise en compte est complètement aberrante :

a) -	Le fait d'autoriser l'exécution d'une appliquette, soit directement soit par signature permet à cette dernière d'avoir un accès à tous l'espace de données du client ce qui me semble être une énorme faille de sécurité.
b) -	Le vocable de "machine virtuelle" pour des applications Java et surtout pour les appliquettes est une usurpation terminologique. En effet, ce n'est pas parce que Java produit du code-machine Java décodé sur toutes les plateformes que ce vocable est justifié. C'est tout juste un shell.
c) -	Pour moi, la gestion de "machines virtuelles" est l'œuvre d'un logiciel de virtualisation qui reproduit exactement et entièrement une machine réelle ce qui n'est pas du tout le cas avec Java.
d) -	Pour ce faire, il me semble que le serveur Java qui assure la sécurité pour lui-même doit pouvoir télécharger une appliquette sur le poste distant en assurant la sécurité pour elle-même dans un contexte d'espace de confinement (un dossier fermé) à l'intérieur duquel elle peut faire tout ce qu'elle veut en terme de stockage de données sans pouvoir en sortir tout en utilisant les possibilité du navigateur internet en guise d'écran, les autorisations étant alors données par un nom d'utilisateur et d'un mot de passe comme c'est le cas habituellement. Plus besoin de signature, un concept complètement à côté de l'objectif. Bien entendu, cet espace de confinement qui est la propriété de l'utilisateur sur son poste de travail, lui est donc accessible d'emblée en lecture et en ecriture.

--ooOoo--