
| Expérimentation OpenScad Modélisation du moto-planeur Fournier RF4 D |
--ooOoo--
 |
Évaluation d'OpenScad |
--ooOoo--
Note de toute dernière minute :
J'ai eu connaissance du logiciel "OpenSCAD" par l'intermédiaire de "FreeCAD" qui propose un atelier "OpenSCAD".
En butinant sur la Toile, je viens de découvrir l'existence le logiciel "OpenJSCAD", de quelques années déjà, apparenté à "OpenSCAD" qui pourrait peut-être très bien répondre au moins en partie aux remarques et aux suggestions que j'ai formulées en fin de page.
Je termine donc mon exposé sur la modélisation de la dérive et de l'empennage du Fournier RF-4 D qui me restent à faire avec "OpenSCAD". J'entamerai ensuite une évaluation de "OpenJSCAD". Il présente l'intérêt d'avoir une version "web" et une version ordinateur sous navigateur Internet.
--ooOoo--
Cette expérience, en vue d'une
impression 3D, fait suite à celles effectuées
d'abord sous FreeCAD (l'horloge
provençale**) puis sous
OpenScad
(le
train épicycloïdal). Cette dernière s'étant révélée intéressante
avec un résultat plutôt satisfaisant pour une première utilisation du logiciel,
 je
me propose de tenter la réalisation d'une petite maquette de décoration de ce
formidable et superbe avion qu'est le Fournier RF4 D,
mon avion préféré, très fréquemment emprunté lors de mon activité
vol à voile et
avion. Cet aéronef étant un
moto-planeur, il me permettait en quelque sorte de pratiquer les deux à la fois.
Il était très agréable à piloter.
je
me propose de tenter la réalisation d'une petite maquette de décoration de ce
formidable et superbe avion qu'est le Fournier RF4 D,
mon avion préféré, très fréquemment emprunté lors de mon activité
vol à voile et
avion. Cet aéronef étant un
moto-planeur, il me permettait en quelque sorte de pratiquer les deux à la fois.
Il était très agréable à piloter.
La réalisation du train épicycloïdal sous OpenScad ne m'a pas posé de problème particulier concernant le logiciel lui-même car les opérations sur les différents composants élémentaires étaient relativement simples. OpenScad n'avait pas été poussé dans ses "derniers retranchements".
La difficulté avait été plutôt d'ordre mathématique. Mes connaissances sur les engrenages étant très très limites, il m'avait fallu puiser dans de la documentation théorique pour appréhender les formules qui lient les différents pignons.
Par contre, la réalisation de la maquette du Fournier RF4 D m'apparait beaucoup plus attractive au niveau de la programmation : les composants sont des surfaces courbes avec des profils non prévues dans le produit. À part sous Blender dans lequel il faudrait construire des maillages comme je l'avais fait pour l'horloge provençale aussi, je me suis reporté sur OpenScad qui m'offrait une programmation apparemment plus accessible et peut-être plus simple que sur FreeCAD avec le langage "Python" sous lequel j'avais étudié le fonctionnement du train épicycloïdal avec animation.
| (**) | Pour une évaluation des produits de modélisation 3D, l'horloge provençale a été modélisée une première fois sous Blender (ICI), puis sous FreeCAD (LA) |
Je me propose donc de décrire le déroulement de cette étude qui me réserve quand même certaines surprises au niveau du logiciel.
N'ayant pas grande expérience du logiciel "OpenScad", j'expose une étude telle que j'ai pu en déduire des différentes documentations auxquelles j'ai pu accéder. Elle vaut ce qu'elle vaut. Il y a peut-être mieux et plus subtile à faire avec des fonctions que j'ignore. Mais bon !...
| Note : | l'absence d'instructions permettant de sortir d'un traitement algorithmique m'a fait renoncer à la prise en charge de l'interpolation entre deux profils. J'en suis donc réduit à utiliser l'instruction "hull" qui interpole linéairement ( voir §4 de "-_Conclusion_:") |
Je ne suis pas sûr que le projet intéresse grand monde en dehors de moi-même mais s'il peut toutefois servir ne serait-ce qu'à une seule personne, en voici toutefois le code-source accessible ICI sans prétendre que c'est un modèle du genre, ni côté programmation, ni côté mathématique.
De mon point de vue, à part certains domaines, souvent à des fins publicitaires, comme les simulations, les animations, l'imagerie virtuelle, le traitement 3D pour la construction d'objets à la maison ou mécaniques me permet plutôt de vérifier si un projet 3 vues conçu et développé avec un bon éditeur 2D ne présente pas d'anomalie de fabrication pour être réalisable.
D'une manière générale, je ne trouve pas un grand intérêt personnel à représenter virtuellement ce qui existe mais, dans le cas présent qui n'est qu'une étude, il faut considérer l'image des trois vues de l'avion Fournier RF4-D, qui existe réellement, comme un projet-dessin à vérifier en vue d'en faire une maquette.
- L'outil de base : les courbes de Bézier :
Les profils et les cadres sont générés avec des courbes de Bézier d'ordre 3. Cubiques, elles sont donc définies par quatre points de contrôle.
Soit donc les 4 points de contrôle P0(x0,y0), P1(x1,y1), P2(x2,y2), P3(x3,y3) et "t" le paramètre variant dans l'intervalle ouvert ]0,1[ dans le plan. On a le système paramétrique suivant auquel la formule de la cote est ajoutée pour que la courbe soit gauche dans l'espace :
| { |
|
Une question se pose : comment réaliser des courbes sous OpenScad qui ne les a pas prévues ?...
Et pour cause !... un point est une entité mathématique servant à la construction d'entités de dessin qui n'ont pas de réalité physique.
C'est en les assemblant que l'on peut déboucher sur une réalisation. J'ai donc choisi la primitive "sphere" du logiciel avec un petit rayon pour matérialiser le point. Ainsi donc, il est très aisé de "dessiner" une courbe de Bézier dans l'espace formés de petits points comme dans l'exemple ci-après.
En premier lieu, soit la fonction :
|
function formule_Bezier(t, points_controle) = points_controle[0]* (1 - t)*(1 - t)*(1 - t) + points_controle[1]*3*t* (1 - t)*(1 - t) + points_controle[2]*3*t*t* (1 - t) + points_controle[3]* t*t*t ; appelable comme suit : t = v ; // une valeur du paramètre entre 0. et 1 ptctrl = [v0, v1, v2, v3] ; // tableau de 4 des points de contrôle resp = formule_Bezier(t, ptctrl) ; // valeur retournée de la coordonnée |
Cette fonction, appliquée à chaque coordonnée, donne sa valeur pour une valeur donnée du paramètre "t".
En second lieu, soit le module qui appelle le primitive "sphere" :
|
module Bezier_0( c // tableau des coordonnée des 4
points de contrôle , rayon // rayon de la sphère qui matérielise la courbe , tpas // pas de balayage sur le paramètre "t" ) { for (t = [0 : tpas : 1.0001]) { x = formule_Bezier(t, c[0]) ; y = formule_Bezier(t, c[1]) ; z = formule_Bezier(t, c[2]) ; translate([x, y, z]) sphere(r=rayon) ; } // => Fin du for (t = [0 : tpas : 1.0001-tpas]) } // => fin du module "Bezier_0" |
En troisième lieu, soit l'appel au module donnant la courbe de Bézier dans l'espace :
|
Bezier_0([ [ 0, 100, 200, 300] , [ 150, 50, 80, 150] , [ 10, 75, 30, 150] ] , 2, 0.025) ; |
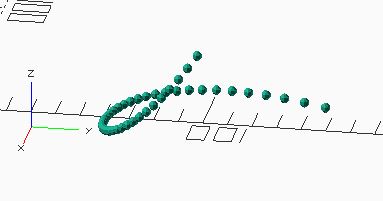
Mais, pour obtenir une ligne continue, il est hors de question de réduire le pas de balayage de la courbe car le résultat serait aléatoire en opérant des zooms et demanderait alors beaucoup de calculs.
La primitive "hull" permet d'interpoler linéairement entre deux sphères matérialisant deux points pour réaliser une coque c'est à dire un cylindre terminé par une demi-sphère à chaque extrémité.
Le module "Bezier_0" devient alors le module "Bezier" qui suit :
|
module Bezier_0( c // tableau des coordonnée des 4
points de contrôle , rayon // rayon de la sphère qui matérielise la courbe , tpas // pas de balayage sur le paramètre "t" ) { for (t = [0 : tpas : 1.0001-tpas]) { hull() // on génère la coque entre deux points consécutifs { // - On détermine la sphère du point pour le paramètre "t" : union() { x = formule_Bezier(t, c[0]) ; y = formule_Bezier(t, c[1]) ; z = formule_Bezier(t, c[2]) ; translate([x, y, z]) sphere(r=rayon) ; } // - On détermine la sphère du point pour le paramètre "t+tpas" : union() { x = formule_Bezier(t+tpas, c[0]) ; y = formule_Bezier(t+tpas, c[1]) ; z = formule_Bezier(t+tpas, c[2]) ; translate([x, y, z]) sphere(r=rayon) ; } } // => Fin du hull } // => Fin du for (t = [0 : tpas : 1.0001-tpas]) } // => fin du module "Bezier" |

| Remarque : | les deux primitives "union"
marquées en rouge sont normalement inutiles dans la logique puisqu'il
n'y a qu'un seul élément "sphere". Après avoir tâtonné pendant un bon bout de temps pour comprendre les "warnings" de compilation ci-dessous :
qui entraînaient une malfonction du module, J'ai fini par ajouter ces deux instructions "union" pour isoler les variables "x", "y" et "z", les accolades toutes seules n'y faisant rien !... Ce souci m'a donc entrainé vers une évaluation d'Openscad dans la "Conclusion". D'autres difficultés sont apparues par la suite. |
- Déroulement du projet
Pour élaborer le projet, un plan 3 vues de l'aéronef ci-dessous est récupéré sur la Toile puis un peu arrangé car un peu faux pour éviter les copies. Le logiciel "Inkscape" utilisant aussi les courbes de Bézier cubiques aide bien pour la détermination de toutes les mesures des données.
Malheureusement, ce très bon produit n'est pas un éditeur de dessin technique seulement d'imagerie car on peut constater les défauts de régularité du maillage portant sur la localisation approximative des points de contrôle des courbes sur un plan déjà lui aussi approximatif. Les intersections, les perpendiculaires quelconques, les parallèles quelconques, etc..., sont évaluées visuellement et non calculées. À cause de cela, le travail est fastidieux !...
C'est pourquoi je cherche désespérément un éditeur de dessin technique, par exemple de type "microCADAM", hélas obsolète,, moins puissant que ce que l'on connaît mais de grâce, intuitif, la première qualité, remplissant 80% des besoins des utilisateurs dans 80% des cas avec 20% des fonctionnalités généralement fournies mais utiles.
J'ai bien essayé "LibreCAD". Ce fut sans succès vu que le logiciel, d'une part, traite les courbes Spline et non Bézier, et surtout d'autre part, il n'est pas du tout intuitif comme tous les clones d' "AutoCAD". Une utilisation interrompue pendant quelques semaines entraîne un réapprentissage fastidieux et désagréable du logiciel. À la retraite, on ne reste pas très longtemps sur ce type de programme comme c'était le cas durant mon activité où, tous les jours, je travaillais sur "Autocad", surtout sous "CADAM". C'était il y a plus de 20 années !...
1°) Modélisation du saumon de l'aile gauche :
C'est la partie la plus simple.
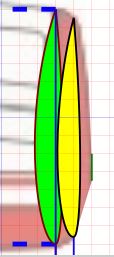 Comme
la fonction "hull"
interpole linéairement entre deux profils, un profil intermédiaire en jaune se
glisse entre le profil de jonction de l'aile et du saumon (en vert clair) et le
bout du saumon (en vert foncé) pour un meilleur aspect. Ce saumon comportera
néanmoins des facettes.
Comme
la fonction "hull"
interpole linéairement entre deux profils, un profil intermédiaire en jaune se
glisse entre le profil de jonction de l'aile et du saumon (en vert clair) et le
bout du saumon (en vert foncé) pour un meilleur aspect. Ce saumon comportera
néanmoins des facettes.
Le pivot de chaque profil est choisi à son bord de fuite. Pour faciliter la prise de mesure, chaque profil est reporté sur l'origine de la page "Inskscape" donnant ainsi directement la valeur des coordonnées des points à saisir.
Chaque profil est défini par deux courbes de Bézier, une pour l'extrado et l'autre pour l'intrado qui se projettent sur le plan XoY suivant une droite. Comme aucune contraire est posée sur sa forme, chaque profil aurait pu être définie par une seule courbe de Bézier qui revient sur elle-même.
En bout de saumon, les deux courbes de Bézier sont réduites à deux droite.
Chaque profil est défini par un appel au module "Bezier" comme dans l'exemple montré plus tôt :
module
aile_gauche_profil_jointure_aile_saumon(tpas)
{ // extrado
Bezier([[ 0.0, 0.0, 0.0, 0.0] , [
0.0, 6.0, 13.0, 13.0] , [ 0.0, 1.5, 1.0, 0.0]] , rayon , tpas) ;
// intrado
Bezier([[ 0.0, 0.0, 0.0, 0.0] , [
13.0, 13.0, 3.5, 0.0] , [ 0.0, -0.5, -0.5, 0.0]] , rayon , tpas) ;
}
module aile_gauche_profil_saumon_milieu(tpas)
{ // extrado
Bezier([[ 0.0, 0.0, 0.0, 0.0] , [ 0.0, 5.5, 12.0, 12.0] , [ 0.0, 1.5, 0.7, 0.0]]
, rayon , tpas) ;
// intrado
Bezier([[ 0.0, 0.0, 0.0, 0.0] , [ 12.0, 12.0, 5.5, 0.0] , [ 0.0, -0.5, -0.6,
0.0]] , rayon , tpas) ;
}
module
aile_gauche_profil_saumon_embout(tpas)
{ // extrado
Bezier([[ 0.0, 0.0, 0.0, 0.0] , [ 0.0, 0.0, 1.5, 1.5] , [ 0.0, 0.0, 0.0, 0.0]] ,
rayon , tpas) ;
// intrado
Bezier([[ 0.0, 0.0, 0.0, 0.0] , [ 1.5, 1.5, 0.0, 0.0] , [ 0.0, 0.0, 0.0, 0.0]] ,
rayon , tpas) ;
}
 saumon semi-transparent |
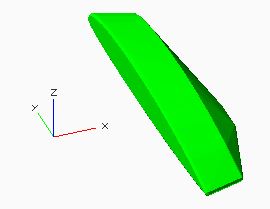 saumon opaque |
2°) Modélisation de la partie courante de l'aile gauche :
Le profil de l'aile au niveau de la jointure avec son emplanture est courbe comme le montre les figures ci-dessous.
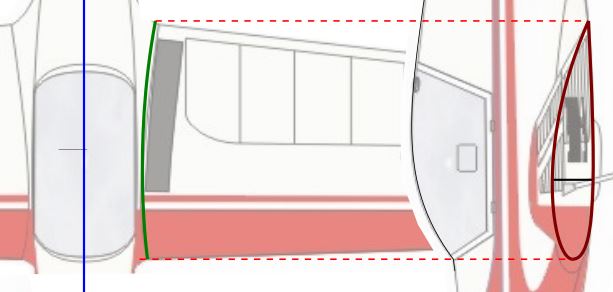
Le profil (en marron) se projette verticalement suivant une courbe (en
vert)
pour suivre le plan.
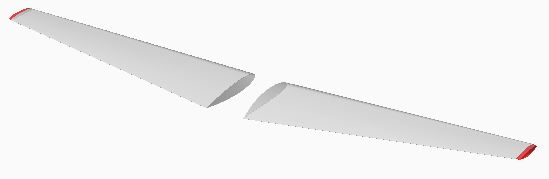
Les ailes avec leurs saumons en semi-transparent pour voir le profil
d'emplanture
3°) Modélisation de la jonction de l'emplanture de l'aile gauche avec l'emplanture du fuselage :
C'est à priori l'une des partie les plus délicate qui réalise le filet entre l'aile et le fuselage au niveau de la partie basse du cockpit.
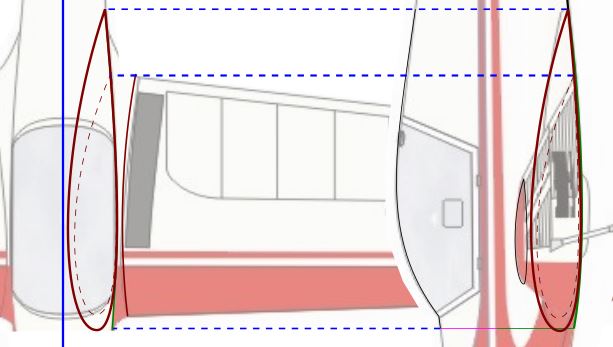
Le profil (en marron) se projette verticalement suivant une courbe (en
vert)
qui épouse la même courbure que l'intrado pour suivre le plan du dessous et du côté du fuselage.

La jointure de l'emplanture avec le fuselage (en rouge comme le saumon)
4°) Modélisation de la partie inférieure du demi-fuselage de la queue :
A - sous le cockpit :
La partie inférieure du fuselage est verticale sur le coté et horizontale dessous à partir des ailes jusqu'à la queue mais on ne garde ici que la partie qui permet de fixer les ailes au fuselage et abritant le train d'atterrissage.
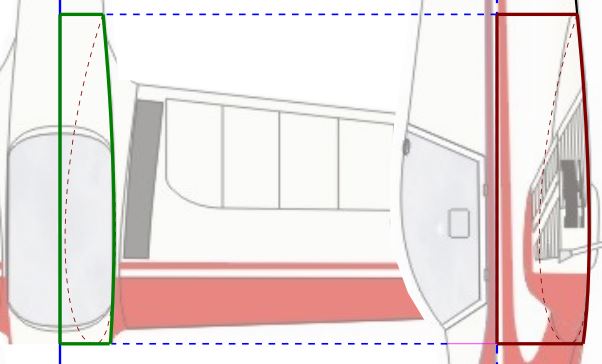
Le profil en marron se projette verticalement sur
le côté du fuselage qui est courbe (en vert).
Le même profil en marron se projette
aussi verticalement sur l'axe du fuselage
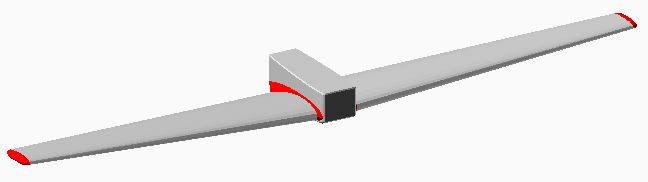
la position de la partie du fuselage sous le cockpit
B - la queue :
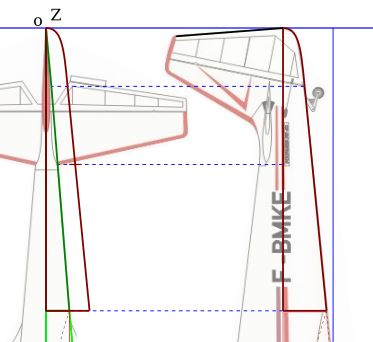
Même commentaire que précédemment.
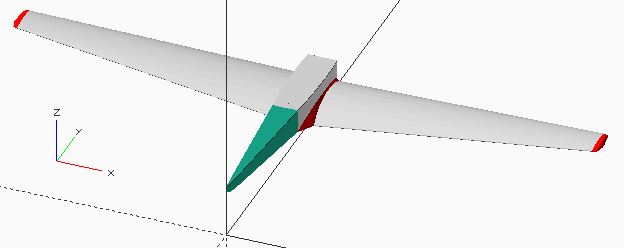
5°) Modélisation de la partie supérieure du demi-fuselage de la queue :
La génération de la partie supérieure du fuselage de la queue repose sur deux cadres interpolés linéairement par la primitive "hull", l'un composé de deux demi arcs de courbes de Bézier à 63 millimètres et l'autre réduit à un segment de droite à 0 millimètre.

Vue symétrique des deux cadres formant le volume de la queue
La génération s'effectue parallèlement à l'axe des "Y" contrairement à celle de la partie inférieure qui s'effectue parallèlement à l'axe des "X" ce qui donne le rendu ci-dessous :
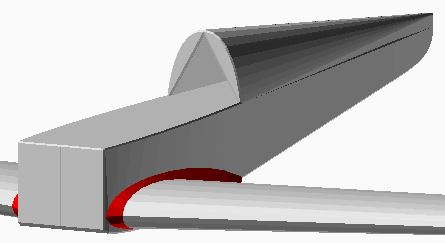
On peut remarquer deux anomalies concernant la primitive "hull" reportées dans les § 5 et 6 de la conclusion :
la primitive ignore la concavité des surfaces.
les deux volumes ne se superposent pas exactement.
Je n'ai pas réussi à corriger. Pourtant, la surface de contact est bien
générée linéairement sur les deux volumes !... Je pense que cela vient du fait que la
primitive "hull"
n'interpole pas de manière affine entre le cadre à 63 mm et celui réduit à
un segment de droite à 0 mm. Elle interpole entre le cadre et une extrémité
du segment, puis elle bouche verticalement ce qui est surprenant.
Pour tenter de corriger, j'ai essayé de prendre en charge l'interpolation entre les deux profils Bézier. Deux manières de procéder sont alors très très proches :
⇒ on applique la primitive "hull" sur deux points consécutifs de chaque profil pour obtenir deux petits cylindres élémentaires sur lesquels on applique à nouveau la primitive "hull" ce qui provoque un bandeau de surface entre les deux profils. On répète l'opération sur tous les autres points des profils. Le résultat obtenu est plus conforme à ce que l'on attend : la surface intérieure est bien régulière.
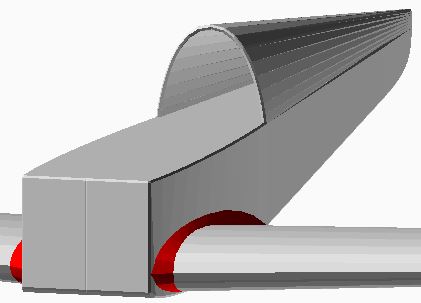
⇒ on applique la primitive "hull" sur un point de chaque profil pour obtenir un cordon cylindrique entre les deux profils. On opère de même sur le point suivant de chaque profil pour obtenir un nouveau cordon cylindrique. On applique à nouveau la primitive "hull" ce qui provoque un bandeau de surface entre les deux profils. On répète l'opération sur tous les autres points des profils. Le résultat obtenu est quasiment identique au précédant.
Mais à bien regarder, il semblerait que c'est plutôt la génération de la surface qui donne l'impression d'erreur. À voir donc :

J'imagine que les trois méthodes sont équivalentes au niveau des temps de calcul. D'ailleurs, ces derniers commencent maintenant à être un peu longs si l'on vide le cache.
la génération du reste du fuselage va se réaliser avec l'une des deux dernières méthodes.
6°) Modélisation du cockpit :
Avec la même manière de procéder, la modélisation du cockpit se présente comme suit :

Vue symétrique du cockpit
6°) Modélisation du capot moteur :
Là aussi, avec les mêmes outils, la modélisation se présente comme suit:
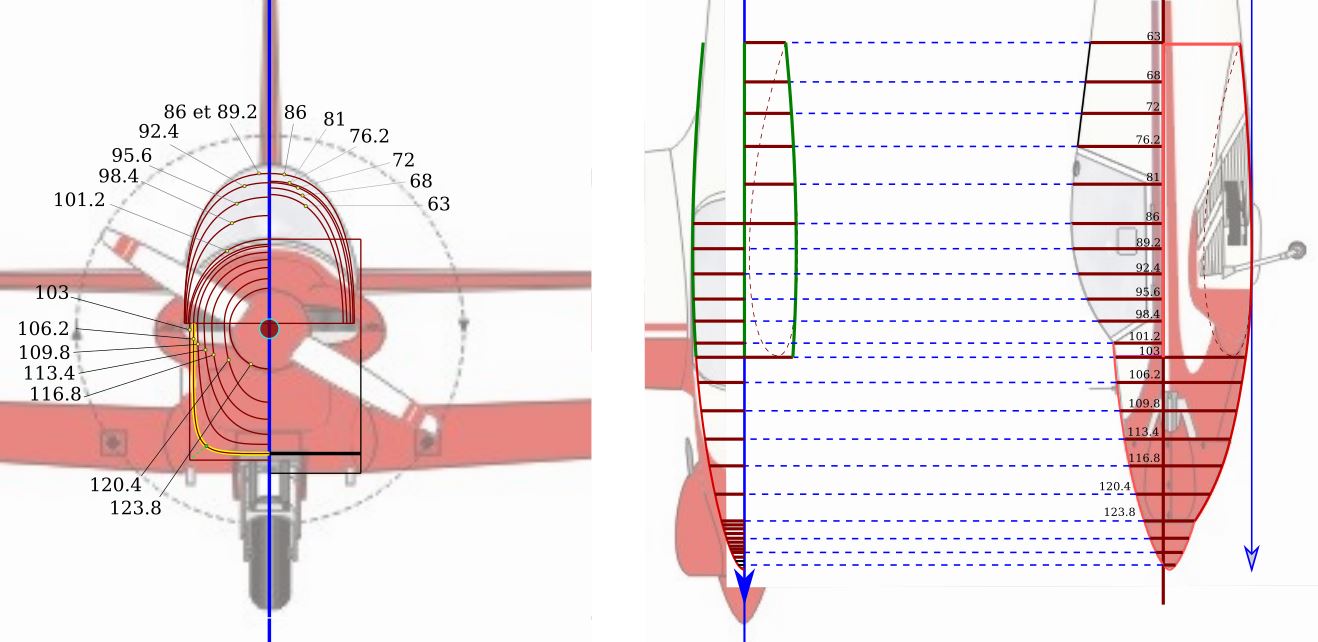
L'image récupérée est un support approximatif.
Les prises de mesures le sont donc aussi
pour donner un résultat qui commence à prendre tournure.

6°) Modélisation de la verrière :
Elle ne pose aucun problème avec les même outils :

si ce n'est une anomalie qui s'estompe suivant l'orientation. Je n'est pas réussi à enlever le panneau blanc dans l'axe de la verrière :
Je me demande si ce n'est pas un problème aux limites avec la primitive "hull" !...
7°) Modélisation des entrées d'aération du moteur :
Là visualisation des entrées-moteur est correcte vu du côté bâbord en retrait arrière

mais dans la vue ci-dessous, le disque de l'hélice masque partiellement l'entrée bâbord malgré la transparence et ceci après application de la symétrie.

Je n'ai pas réussi à corriger et où trouver l'erreur s'il y en une.
8°) Modélisation de la dérive et de l'empenage :
Pas de problème pour la dérive et l'empennage.

| 1 - | lors de l'écriture de la fonction
"formule_Bezier",
j'ai été extrêmement surpris de lire qu'une fonction
OpenScad
n'admet qu'une formulation mathématique ce qui interdit
tout découpage et tous traitement algorithmique. Impossible donc de découper la formule, ni même d'effectuer un choix si le calcul admet plusieurs solutions !... Les formules de Bézier étant cubiques, j'ai dû renoncer au développement assez acrobatique de la résolution d'une équation du 3ème degré pour une racine réelle sans pouvoir faire une incursion dans les nombres complexes afin de déterminer les deux autres racines réelles si elles existent !... |
||
| 2 - | Les instructions "union"
inutiles : dans la documentation "pdf" du logiciel de Rudy Giot, il est
explicitement écrit :
Je dois avouer que cela m'a fait sursauter. Pourquoi ce choix technique ?... il me paraît complètement incohérent. Une compilation est un outil essentiellement fait pour construire un objet actif. C'est donc bien là la raison des "warnings" cités plus haut. La compilation ne comprend donc pas que les coordonnées "x", "y" et "z" puissent être modifiées coup sur coup. |
||
| 3 - | J'ai rencontré un gros soucis avec la portée des variables. Un module ne reconnaît que les variables qu'il a créées et ignore complètement de ce fait les variables en retour déclarées dans la partie appelante du programme (il n'y a pas de déclaration explicite du programme principal). La notion de variable globale n'existe pas. Un module ne peut donc pas renvoyer une valeur. | ||
| 4 - | une autre surprise est venue du fait qu'il n'existe pas d'instruction permettant d'interrompre un cycle itératif : pas d'instruction "break" ni "goto" ce qui interdit tout traitement algorithmique !... | ||
| 5 - | un petit souci avec la primitive "hull" qui interpole entre les parties proéminentes d'un volume concave provoquant une visualisation erronée. c'est le cas de la jointure aile-fuselage. | ||
| 6 - | la primitive "hull" n'interpole pas de manière affine entre un profil courbe et un segment de droite. |
- Quelques suggestions :
| 1 - | Spécifiée à l'alinéa 2 de la conclusion, revenir à un comportement sain d'affectation des variables au moment de l'exécution et non de la compilation. Les développeurs de ce pseudo-langage semblent avoir conservé leurs réflexes de Programmation Orientée Objets et par du tout celle d'Exécution Orientée Objets !... | ||
| 2 - | Introduction
d'instructions de rupture d'itérations : les instructions "break",
"continue" "switch" du
langage C
conviennent parfaitement, et même l'instruction "goto"
tant décriée (!!!). Nul besoin d'en créer d'autres.
|
||
| 3 - | Prise en compte par l'instruction "hull" des concavités et convexités des volumes pouvant être creux, ouverts ou fermés. | ||
| 4 - | Traiter les cercles comme des ellipses sans avoir besoin de recourir à une primitive "scale". | ||
| 5 - | ajouter une primitive 3D "curve3D". sous la forme d'un cordon à base elliptique donné, ouvert ou fermé soit par un plan, soit une demi-ellipse. Les courbes de Bézier me semblent assez pratiques par leur simplicité et leur facilité de manipulation des points de contrôle. | ||
| 6 - | ajouter une primitive 2D "curve2D" pour pouvoir les utiliser avec les primitives "extrude". Les courbes de Bézier me semblent là aussi assez pratiques par leur simplicité. | ||
| 7 - | permettre la programmation dans les fonctions et non une simple formulation. | ||
| 8 - | prise en compte de variables globales voire des arguments de module en retour, |
- En aparté :
Pour moi bien sûr, le langage mis à disposition est une mauvaise inspiration du langage C, pas du tout à la hauteur des prétentions du logiciel à moins qu'il ait été écrit pour l'initiation scolaire au 3D.... Un langage de plus dirais-je !...
De mon expérience informatique qui a débuté au
tout début des années 1960,
 mon tout premier langage en faculté fut l'"Algol"
dont j'ai gardé le livre comme une relique. On pourra remarquer que sa sémantique lexicale
est proche de celle du langage C
qui s'en est inspiré comme le montre
l'exemple
ICI.
mon tout premier langage en faculté fut l'"Algol"
dont j'ai gardé le livre comme une relique. On pourra remarquer que sa sémantique lexicale
est proche de celle du langage C
qui s'en est inspiré comme le montre
l'exemple
ICI.
Il
s'en est suivis l'apprentissage et l'usage d'autres langages de
programmation : différentes versions du "Fortran", orienté
scientifique,
du "Cobol"
orienté gestion
puis du
"PL/1" d'IBM
puisque je faisait partie de l'équipe-système de développement et de
maintenance des différents moniteurs VM, CMS, MVS, OS
390/Open Edition, prétendu orienté les deux, du
"Pascal", du
langage "C" et
"C++"
sur les stations de travail Unix. Enfin à
la retraite, je continuai avec "Python" (animation sous
FreeCAD),
"Java" pour les
applets Sun et la programmation "Java" sous
Android).
Depuis les années 1970, j'ai donc pu vivre une prolifération de sectes informatiques (c'est comme cela que je le ressens, ce n'est qu'un point de vue !...) tendant à imposer une vision intégriste de leurs langages prétendus supérieurs aux autres, des "ersatz" du langage C, se gargarisant de Programmation Orientée Objet, oubliant complètement que, d'une part, le plus important est l'Exécution Orientée Objet (illustration le "Noyau Graphique d'Images Structurées") et que, d'autre part, on vit tout naturellement dans un environnement orienté objets depuis le "Big bang" il y a 13 milliards d'années !... Ce n'est donc pas une révolution. Je ne polémiquerai donc pas sur les positions dogmatiques des "anti-goto", les "anti-instruction-system()", des "anti-pointeurs" voire même des "anti-allocation dynamique-mémoire" !...
Pour revenir à OpenScad, même pour des scolaires, je reste cependant bien dubitatif sur certains choix techniques du langage proposé,
choix techniques très surprenants et très handicapants.
| Dommage !... car l'idée de proposer un logiciel 3D directement programmable était séduisante, la présentation de l'imagerie étant bonne, suffisante et facile à manier. tout cela, sans être obligé de passer par des logiciels plus lourds comme Blender, FreeCAD, AutoDesk, etc... dont beaucoup sont payants. |
--ooOoo--