
de John Bisby
virtualisation sous FreeCAD
Fichier "Diametroid.FCStd"
aoüt
2014
modifié .. .. ....
 |
Le Diametroid de John Bisby virtualisation sous FreeCAD Fichier "Diametroid.FCStd" |
--ooOoo--
Le logiciel FreeCAD, un peu comme les logiciels 3D Blender, AutoDesk123D, Rhinoceros, tout comme les logiciels 2D DraftSight, ProgeCAD, Solid Edge que j'ai pu un peu expérimenter, a une difficile et délicate prise en main surtout parce qu'il manque d'intuitivité. On peut le constater dans les forums par le nombre de questions posées sur des sujets assez simples en général. Mais, passée cette petite période un peu désagréable, le logiciel s'apprend tranquillement avec patience.
Comme beaucoup, je n'ai pas échappé à cette petite période de 'pataugeage'. C'est pourquoi j'ai essayé tant bien que mal de décrire les opérations pour pouvoir m'y référer plus tard car je n'ai pas vocation à m'en servir tous les jours. J'ai fini enfin par réaliser, un peu à tâtons, ma première petite virtualisation de ce Diametroid dont je présente à nouveau l'illustration ci-après avec ses trois parties principales :
Pour manipuler sous FreeCAD, j'ai passé un bon moment sur les différents ateliers pour entrevoir les différentes possibilités et en particulier ici :
en principe les seuls dont on a besoin pour le moment.
I - Préparation
| Une recommandation préalable : durant les manipulations, il est utile de sauvegarder l'évolution de la modélisation à chaque point de crédibilité car les erreurs sont fréquentes et le logiciel ne revient pas parfaitement à l'état précédent. |
On se servira du coloriage des pièces pour bien les différencier et mieux voir aussi leurs associations quand c'est possible.
- Définition de la nomenclature du Diametroid :
Pour faciliter l'identification des composants, il s'agit de composer en premier une nomenclature de la transmission, chose que je n'avais pas vu tout de suite.
Quand on lance le logiciel, que l'on ouvre un nouveau fichier, et que, ici, on l'enregistre sous le nom de "Diametroid.FCStd", on a le panneau ci-dessous si on a pris soin d'afficher la "vue combnée" (Affichage=>Vues=>Vue combinée) dont on aura recours en permanence. On remarquera que le nom du fichier 'Diametroid' est reproduit dans la fenêtre comme un répertoire de l'"Application". C'est la nomenclature qu'il s'agit d'initialiser :
En pointant la souris sur ce nom et en pressant le bouton droit, il apparaît une fenêtre contenant "Créer un groupe...'. C'est ainsi que l'on va créer la nomenclature du Diametroid en renommant (bouton droit=>Renommer) le nom "GroupeNNN" automatiquement généré "NNN" étant un numéro de séquence. On obtient alors la nomenclature suivante :
Ainsi, on retrouve donc la nomenclature des pièces spécifiées dans la figure 1 comme suit :
| - | 1 | Train_epicycloidal_entree_planetaire | : | Planétaire du train épicycloïdal d'entrée | |
| - | 2-3 | Train_epicycloidal_entree_satellite_1 | : | 1er satellite du train épicycloïdal d'entrée | |
| - | 2-3 | Train_epicycloidal_entree_satellite_2 | : | 2ème satellite du train épicycloïdal d'entrée | |
| - | 4 | Train_epicycloidal_entree_support_satellites | : | Support des satellites du train épicycloïdal d'entrée | |
| - | 5-6 | Train_epicycloidal_entree_couronne_satellites | : | Couronne des satellites du train épicycloïdal d'entrée | |
| - | 7 | Pignon_de_phase | : | Pignon de phase | |
| - | 8 | Bloc_diametroid | : | Bloc carter du Diametroid | |
| - | 9 | Flasque_support_couronne_sortie | : | Flasque du support de la couronne du train épicycloïdal de sortie | |
| - | 10 | Train_epicycloidal_sortie_couronne_satellites | : | Couronne des satellites du train epicycloidal de sortie | |
| - | 11 | Train_epicycloidal_sortie_support_satellites | : | Support des satellites du train épicycloïdal de sortie | |
| - | 12 | Train_epicycloidal_sortie_satellite_3 | : | 3ème satellite du train épicycloïdal de sortie | |
| - | 12 | Train_epicycloidal_sortie_satellite_2 | : | 2ème satellite du train épicycloïdal de sortie | |
| - | 12 | Train_epicycloidal_sortie_satellite_1 | : | 1er satellite du train épicycloïdal de sortie | |
| - | 13 | Train_epicycloidal_sortie_planetaire | : | Planétaire du train épicycloïdal de sortie | |
| - | Elements_construction | : | les objets (points, lignes, cercles) de construction |
Le groupe "Element_construction" sera alimenté tout au long de la modélisation. Les éléments permettent de localiser exactement les composants de la transmission.
Un composant de la nomenclature est affichable ou masqué en positionnant la souris sur son nom et en cliquant sur bouton droit puis en choisissant "Afficher la sélection" ou "Masquer la sélection" ou en utilisant le raccourci "barre d'espace"
- Création de l'axe de référence du Diametroid :
il est matérialisé par la ligne des arbres d'entrée et de sortie. On trace donc une ligne pointillée définie par les points suivants le long de l'axes des Z :
Pour se faire :
Un panneau s'affiche alors pour la saisie des coordonnées de l'origne puis, après validation, un deuxième pour la saisie des coordonnées de l'extrémité. Une entrée "LineNNN" est crée en fin de liste dans la nomenclature.
II - Modélisation du pignon planétaire du train épicycloïdal d'entrée
- Création du pivot de l'engrenage :
il est matérialisé par un point rouge :
Un panneau s'affiche alors pour la saisie des coordonnées du point. Les coordonnées proposées
sont celles de l'origine des axes de référence. On garde ces coordonnées et après validation, une entrée "PointNNN" est crée en fin de liste dans la nomenclature.
- Création de l'engrenage du planétaire :
Il est matérialisé par un profil d'engrenage :
Une entrée "InvoluteGear" est crée en fin de liste dans la nomenclature et le profil de l'engrenage est dessiné dans le plan XY à Z=0 (figure 4) à faire apparaître distinctement. Mais là, l'entrée crée et le groupe récepteur "Train_epicycloidal_entree_planetaire" ne sont pas visibles ensemble dans la fenêtre de la nomenclature. On ne peut donc pas la glisser. Si on clique sur l'entrée avec le bouton droit, on constate que l'option "Couper" (Cut) n'est pas délectable. Dommage !... car il faut procéder autrement :
 Figure 4 |
==> |
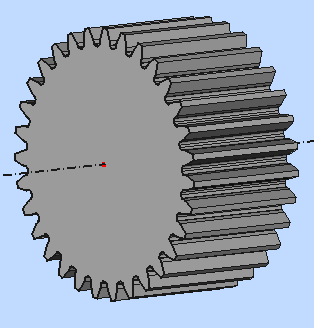 Figure 5 |
Cet engrenage est fixé à un arbre. On réalise donc un évidement de 30 mm de diamètre.
Pour cela, on procède, cette fois avec un cylindre de
30 mm et de
30 mm de longueur que l'on
peut créer avec l'outil "Cylindre"(![]() )
de la barre d'outils de l'atelier "Pièce"
(Part). Une entrée "CylindreNNN" est
créée dans la nomenclature et un petit cylindre de 2 mm de rayon est
affiché dans le dessin ayant le même pivot que l'engrenage.
)
de la barre d'outils de l'atelier "Pièce"
(Part). Une entrée "CylindreNNN" est
créée dans la nomenclature et un petit cylindre de 2 mm de rayon est
affiché dans le dessin ayant le même pivot que l'engrenage.
Une entrée "CutNNN" est créée dans la nomenclature. Il faut donc la migrer et la renommer dans le groupe Train_epicycloidal_entree_planetaire" . On obtient l'image de la figure 6 ci-après.
- Création de l'arbre de l'engrenage du planétaire :
C'est tout simplement un cylindre de 15 mm de diamètre et de 80 mm de long qui rentre de 10 mm dans l'évidemment de l'engrenage. On procède comme précédemment mais, cette fois-ci, on opère un décalage de -65 mm le long de l'axe des Z comme on peut le voir sur la figure 9 ci-après.
On le colorie en vert pour agrémenter l'image avec l'onglet "Vue" des "Propriétés (figure 7).
 Figure 6 |
==> |
 Figure 7 |
L'image de la figure 7 donne une idée de FreeCAD avec l'image du planétaire et de son arbre sans aucune fioriture : pas de fillet, ni de chamfrein, etc....
Dans le premier jet de découverte, j'avais continué la virtualisation jusqu'au bout et ce n'est qu'ensuite que j'avais attaqué l'animation du Diametroid.
Ici, je mène la virtualisation et l'animation en parallèle tant que c'est possible (ICI).
III - Modélisation des pignons satellite du train épicycloïdal d'entrée :
La position du pivot de l'engrenage dépend de la taille de cet engrenage qui doit s'engrener dans les dents du planétaire modélisé dans le paragraphe précédent. C'est pourquoi on commence par le déterminer.
- Création de l'engrenage du satellite n°1 :
On procède, comme pour le planétaire, à la détermination du profil d'engrenage à partir de l'option "InvoluteGear" de l'atelier "Part Design".
Le profil est centré sur le pivot du planétaire. On le décale donc de 58 mm positivement le long des y. Mais les dents ne sont pas forcément engrenées. On effectue donc une petite rotation de 1°.
Pour ce faire, on sélecte l'entrée "InvoluteGear" créée à la fin de la nomenclature et on s'intéresse aux "Propriétés" de ce profil dans l'onglet "Données" qui l'on peut modifier directement dans le panneau comme sur la figure 8 :
 Figure 8 |
|
||||||||||||||||||||||||||||||||||||||||||||
- Création du pivot de l'engrenage du satellite n°1 :
il est matérialisé par un point rouge suivant la même procédure que pour le pivot du planétaire. Ce sont les valeurs déterminées par le décalage du profil d'engrenage c'est à dire :
Un panneau s'affiche alors pour la saisie des coordonnées du point. Une entrée "PointNNN" est crée en fin de liste dans la nomenclature.
- Création de l'engrenage du satellite n°2 :
On procède, comme pour le satellite n°1, mais avec un décalage différent, à l'opposé par rapport au planétaire :
On les colorie avec une couleur qui peut se vouloir être un vert métallique, pour différencier et agrémenter ("Vue" des "Propriétés").
- Création du pivot de l'engrenage du satellite n°2 :
il est matérialisé par un point rouge suivant la même procédure que pour le pivot du satellite n°1. Ce sont les valeurs déterminées par le décalage du profil d'engrenage c'est à dire :
Un panneau s'affiche alors pour la saisie des coordonnées du point. Une entrée "PointNNN" est crée en fin de liste dans la nomenclature.
On obtient la figure 9 ci-dessous sans leurs arbres que l'on dessinera plus tard car ils sont solidaires des excentriques.
avec son animation ICI.
- Création de l'arbre de l'engrenage satellite n°1 :
C'est tout simplement un cylindre de 60 mm de longueur et de 15 mm de rayon positionné à :
- Création de l'excentrique du satellite n°1 :
C'est tout simplement un cylindre de 20 mm de longueur et de 40 mm de rayon positionné à :
- Création de la broche de l'excentrique du satellite n°1 :
C'est tout simplement un cylindre de 20 mm de longueur et de 10 mm de rayon positionné à :
- Création de l'arbre de l'engrenage satellite n°2 :
C'est tout simplement un cylindre de 60 mm de longueur et de 15 mm de rayon positionné à :
- Création de l'excentrique du satellite n°2 :
C'est tout simplement un cylindre de 20 mm de longueur et de 40 mm de rayon positionné à :
- Création de la broche de l'excentrique du satellite n°2 :
C'est tout simplement un cylindre de 20 mm de longueur et de 10 mm de rayon positionné à :
On obtient le résultat de la figure 10 ci-dessous :
dont on peut voir une petite animation ICI.
| Note : | mon premier réflexe fut de générer
l'union de l'excentrique et de la broche des deux satellites. Mais après
quelques essais, j'ai eu quelques soucis pour manipuler les broches non
pas pour la modélisation résente mais pour la suite où ces broches
doivent s'emboîter dans les évidements de la couronne. Comme cela ne présente aucune difficulté mathématique, j'ai donc préféré laisser broches et excentriques séparés pour calculer directement dans le script la position de chaque broche afin de pouvoir y accéder plus facilement. |
Pour en arriver jusque-là, il m'a fallu passer quelques moments laborieux surtout en ce qui concerne la définition de la nomenclature du Diametroid. La gestion de la "vue combinée" ("Étiquettes & Attributs") me paraît assez limite, les développeurs en nombre réduit préférant plutôt soigner leur propre énergie, au détriment de celle des utilisateurs en nombre autrement plus conséquent (voir 4° de de la Remarque 1)
IV - Modélisation des pignons satellite du train épicycloïdal de sortie :
On le verra plus en détail dans la page "Animation", mais comment peut-on pressentir le fonctionnement de cette transmission continue variable :
Concrètement, le conducteur adapte un régime moteur pour pouvoir rouler à la vitesse qu'il souhaite. La transmission a donc pour but de sélecter en permanence, sans aide extérieure, le rapport de vitesse approprié pour des efforts minimaux et aussi des contraintes minimales. C'est ce que fait normalement le conducteur manuellement si la boîte est mécanique et ce que fait l'asservissement et l'électronique si c'est une boîte automatique.
La vitesse de translation du véhicule est directement liée à la vitesse de rotation des roues donc à la vitesse de rotation de l'arbre du planétaire de sortie. Donc étant donné une vitesse de rotation du moteur donnée sur l'arbre du planétaire d'entrée et une vitesse de rotation donnée sur l'arbre du planétaire de sortie, il s'agit de déterminer la vitesse de rotation du bloc qui contient l'ensemble des composants qui assurent l'auto-adaptation.
Pour ces composants, j'ai fait un peu différent du Diametroid de John Bisby pour simplifier la modélisation ce qui ne change rien au déroulement de l'analyse de la transmission. Le train épicycloïdal de sortie est identique au train épicycloïdal d'entrée. Pour créer ce train de sortie, j'ai procédé tout simplement à la copie des différents composants puis à modifier leur repositionnement puisqu'ils sont symétriques. Je n'ai pas utilisé la symétrie au niveau de la modélisation pour ne pas avoir à en tenir compte dans le script d'animation.
| Attention : | lorsque l'on copie un
composant polymorphe obtenu à partir d'opérations booléenne, bien
prendre la précaution de conserver tous les éléments qui le composent
pour pouvoir éventuellement agir sur chacun d'entre eux par la suite
ci-besoin. Donc, avant d'opérer ces opérations booléennes, bien prendre la précaution de sauvegarder le projet et s'assurer, à l'issue de l'opération, que les différents sous-composants sont bien présents dans la nomenclature. |
C'est la même procédure pour le support d'excentriques comme sur la figure 11 ci-dessous dont on énumère néanmoins les différentes opérations :
Ces deux copies vont servir à confectionner les deux évidements. L'arbre de maintien maintenant :
À ce niveau, on dispose de tous les ingrédients pour élaborer le support des excentriques du satellite n° 1. On opère maintenant les opérations booléennes ci-après. On rappelle que ces opérations booléennes sont disponibles dans le menu :
"Pièces=>Opération booléenne" ou la barre d'outils appropriée
Pour réaliser l'évidemment de l'excentrique n°2, il suffit de reproduire les mêmes opérations. Pour terminer, renommer les entrées crées pour homogénéité afin de s'y retrouver plus facilement ensuite comme dans l'illustration de la figure 12 ci-dessous à titre d'exemple.
Si l'on opère avec des copies, bien être vigilant pour conserver dans la nomenclature tous les sous-composants d'un composant polymorphe !...
La symétrie s'arrête là car il en est tout autrement dans le bloc contenant les composants d'auto-adaptation.
Lors des essais d'animation, un effet stroboscopique apparaît au niveau des engrenages rendant difficilement détectable leur sens de rotation. Pour mieux voir ces mouvements, sur chaque engrenage, une dent est colorées pour mieux la repérer. Cette opération de coloriage s'effectue comme suit :
Un panneau s'affiche et invite à sélecter une face dont la couleur s'affiche aussitôt et que l'on peut modifier. Sélecter une autre face pour à nouveau changer sa couleur et ainsi de suite. Terminer la série de modification par "Ok"
V - Modélisation de la couronne du train épicycloïdal d'entrée :
 Figure 13 |
Ce composant a une forme assez particulière et un peu élaborée pour un débutant (figure 13 du premier essai de modélisation). C'est pour cela que la description de sa modélisation est décrite en détail pour me remémorer plus tard les procédures si besoin. En effet, si l'on se reporte à la figure 1, on notera que cette couronne correspond aux pièces 5 et 6 à l'intérieur desquelles vient s'appuyer le pignon de phase de 12 dents (7) pour former un train hypocycloïdal tout cela encadré par le support des excentriques d'entrée (4), le bloc (8) solidaires du support des excentriques de sortie (9).
La forme intérieure de cette couronne est spéciale pour permettre sa rotation. On verra que le pignon de phase est solidaire d'une entretoise à la forme imposée pour faire liaison solidaire à travers la couronne entre le support des excentriques d'entrée, le support des excentriques de sorties et le bloc qui les enferme.
L'animation permettra de voir un peu mieux de quoi il retourne.
Cette couronne est formée d'un fond et d'un engrenage de 24 dents.
- Modélisation du fond de la couronne de l'étage d'entrée :
Cette couronne est commandée par les deux broches des deux excentriques d'entrée. Son centre se situe donc au milieu des centres des deux broches. Son rayon va dépendre de la taille de l'engrenage de 24 dents qui, lui, va dépendre à son tour du pignon de phase de 12 dents. Il faut donc combiner toutes ces contraintes, ici visuellement.
pour faciliter le travail, il est bon de masquer tout le train épicycloïdal de sortie.
La première chose à faire est donc de déterminer la taille des deux engrenages du train hypocycloïdal :
Il faut faire coïncider les dents du pignon de phase dans les dents de l'engrenage de la couronne. Pour ce faire, on joue par dichotomie avec les paramètres :
En
 Figure 14 |
| - le profil d'engrenage de la couronne : | ||
| ° "Modules" | = 4 mm, | |
| ° "Number Of Curves" | = 1, | |
| ° "Number Of Teeth" | = 24, | |
| ° "Pressure Angle" | = 22°, | |
| - le profil d'engrenage du pignon de phase : | ||
| ° "Modules" | = 4 mm, | |
| ° "Number Of Curves" | = 1, | |
| ° "Number Of Teeth" | = 12, | |
| ° "Pressure Angle" | = 30°, | |
La taille des engrenages déterminée, il s'agit de définir la taille du fond de la couronne en tenant compte des la position des broches des excentriques. La couronne est située à z=450 mm dans l'éclaté.
On obtient les deux cylindres des broches qui débordent du cylindre de la couronne. On corrige donc le rayon du cylindre de la couronne en modifiant la propriété rayon (80 mm) pour qu'ils soient à l'intérieur.
On procède aux évidements dans le fond de la couronne correspondant aux broches des excentriques :
On obtient un nouveau composant que le logiciel a nommé "CutNNN".
On obtient encore un nouveau composant que le logiciel a nommé "CutNNN".
Le fond de la couronne se présente comme sur la figure 15 en perspective et comme sur la figure 16 en vue de dessus :
 Figure 15 |
 Figure 16 |
Pour la réalisation de l'évidement en forme de cercle rétréci en son milieu, on procède comme suit :
Ces deux cylindres se situent en avant du fond de couronne et centré sur chacun des axes des broches des excentriques.
On obtient les 3 cylindres (numérotés 1, 2 et 3 à gauche) positionnés comme sur les deux images ci-dessous :
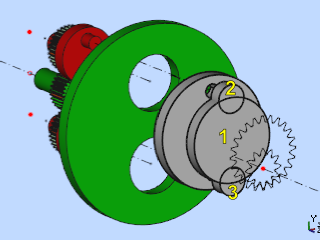 Figure 17 |
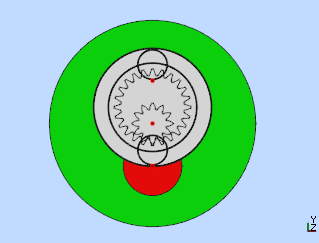 Figure 18 |
Depuis le début de la modélisation de la couronne, un certain nombre d'entrées a été créé dans la nomenclature au niveau du répertoire du projet toutes nommées par FreeCAD en "InvoluteGearNNN", "CylindreNNN", "CutNNN". donc il est préférable de sélecter les objets dans la nomenclature plutôt que sur l'affichage qui ne servira que de confirmation du choix.
Pour obtenir la forme de l'évidement, on procède comme suit :
Une entrée "CutNNN" est créée dans le répertoire du projet.
 Figure 19 |
Une entrée "FilletNNN" est créée.
Répéter l'opération sur les 3 autres arêtes. Des entrées "FillerNNN" sont créées en cascade et on obtient l'image de la figure 19 ci-contre.
Note : si, durant les manipulations, une entrée composite était en erreur, sa suppression entraînerait la restitution de tous ses composants dans le niveau avant la modification.
Reste
 Figure 19 |
Une entrée "CutNNN" est créée.
- Modélisation de l'engrenage de la couronne de l'étage d'entrée :
Cet engrenage a une denture interne. Il faut donc créer un engrenage à denture externe qui représente la forme de l'évidement à réaliser dans un cylindre de la taille du fond de la couronne et collé à lui.
Une entrée "PadNNN" est créée.
- Modélisation de la couronne complètede l'étage d'entrée :
L'opération consiste à associer le fond de la couronne et l'engrenage de la couronne.
Une entrée "FusionNNN" est créée correspondant à la couronne complète du train épicycloïdal d'entrée comme sur les figures 20 et 21 ci-dessous :
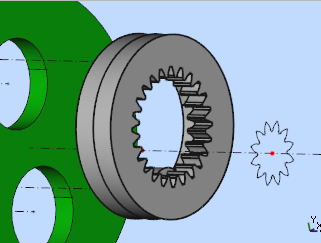 Figure 20 |
 Figure 21 |
Pour terminer l'opération et être homogène pour une meilleure lecture ultérieure, on déplace l'entrée correspondant à la couronne complète "Fusion002" dans mon exemple dans le groupe "Train_epicycloidal_entree_couronne_satellites" et on procède au changement des noms des entrées de la figure 22 à gauche montrant le développement de tous les composants de la couronne pour obtenir ceux de la figure de 23 de droite plus compréhensible :
 Figure 22 |
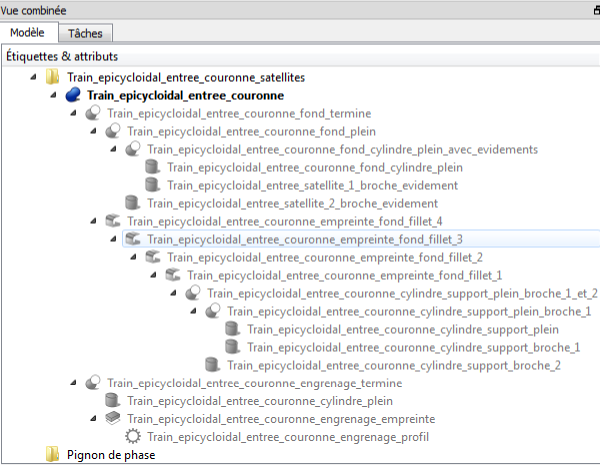 Figure 23 |
Toutes les entrées en gris clair ne sont pas affichées pour l'aspect du rendu de l'image. Cependant les afficher à la demande permet de les localiser. Ainsi, il est possible de retrouver le cheminement pour construire un composant.
En temps normal, il serait surprenant qu'on ait à revenir sur les composants non affichés par FreeCAD ou à les utiliser directement car la seule entrée qui importe est celle de la racine de l'arborescence c'est à dire "Train_epicycloidal_entree_couronne" appelée dans les scripts.
Cette description m'a permis de mieux comprendre le fonctionnement de FreeCAD.
VI - Modélisation du pignon de phase :
 Figure 24 |
Ce pignon centré sur l'axe général du Diametroid se compose de deux parties, l'engrenage à denture externe et l'entretoise qui a aussi une forme particulière puisqu'elle doit évoluer dans l'évidement du fond de la couronne vue précédemment (figure 24 du premier essai de modélisation).
Les différentes phases de la modélisation ne seront pas décrites de manière aussi détaillée que pour la couronne puisque l'on reprend pratiquement les mêmes outils.
- Modélisation de l'engrenage du pignon de phase :
On revient donc sur le profil d'engrenage, "InvoluteGearNNN" dans la nomenclature, que l'on a gardé en réserve. Ce profil avait été positionné sur (x=0 mm, y=0 mm, z=600 mm).
On lui donne du volume par une "Protrusion" de longueur=20 mm et aussi le nom "Pignon_de_phase_engrenage".
- Modélisation de l'entretoise du pignon de phase :
Il faut donner à cette entretoise une forme qui va pouvoir évoluer dans l'évidement du fond de la couronne sans le toucher. Elle doit avoir une forme analogue à celle de l'évidement de la couronne. De plus, l'engrenage de la couronne possède 24 dents, celui du pignon de phase 12 dents. La vitesse de rotation du pignon de phase est double de celle de l'engrenage de la couronne pour qu'à chaque tour, la position de l'entretoise soit la même par rapport à l'évidement.
On procède donc comme suit :
Entraînée par les deux broches des excentriques, la couronne se déplace parallèlement à elle-même en faisant tourner le pignon de phase comme le montre la figure 26.
 Figure 25 |
 Figure 26 |
--ooOoo--
| Lors de
l'écriture du script Python et de l'analyse de l'animation, j'ai détecté
une anomalie de fonctionnement provoquant un blocage mécanique. La virtualisation a donc été interrompue en attendant des éclaircucements. |
--ooOoo--