le Diametroid
Reprise du document de John Bisby
|
|
Créée en Août 2014 |
| Une transmission
continue variable le Diametroid Reprise du document de John Bisby |
--ooOoo- ---------- En cours d'écriture !....---------
La transmission continue variable (CVT) proprement dite
:
Le "diametroid"
En lisant la documentation technique de John Bisby que j'ai pu obtenir sur la Toile, je n'ai pas très bien réussi à saisir le fonctionnement complexe de cette transmission.
En effet, si je comprends parfaitement l'existence des deux trains épicycloïdaux d'entrée et de sortie, je ne comprends pas du tout par quelles lois physicomathématiques les composants du mécanisme central d'auto-adaptation des couples de puissance s'adaptent aux efforts et contraintes émises par le deux trains. L'analyse de la documentation devrait en principe apporter l'éclairage sur ces lois physicomathématiques.
Elle est écrite en anglais :
de John Bisby
| Entrée => |
 |
Sortie => |
Pour comprendre le mieux possible la documentation de John Bisby, fallait-il donc faire une traduction pure et dure du projet ? Je ne le crois pas. J'ai choisi de la reprendre sans la plagier et de lui adjoindre des informations complémentaires.
Le but de cette rubrique est donc d'exposer mon analyse plus en profondeur en tâchant d'en traduire le mieux possible l'esprit.
Les informations rajoutées sont notées en caractères roses et italiques dans la présente police (Times New Roman).
| Page 1 de garde |
Diametroid
Le Saint Graal (le trésor)
de la transmission de puissance
Auteur : John Bisby
Pour faciliter la compréhension laborieuse du document un certain nombre d'informations et d'illustrations ont été ajoutées à partir d'analyses effectuées avec d'autres logiciels comme FreeCAD en particulier.
| Page |
Introduction
Le Diametroid est un type entièrement nouveau de transmission mécanique, désigné par sa caractéristique principale : Seuil Dynamique - Transmission à Variation Continue (TVC-SD). Comme le montre la figure 1, le Diametroid ne se fixe pas sur un châssis de montage ou une superstructure. Ses arbres de rotation d'entrée et de sortie soutiennent physiquement la transmission seulement s'ils ont la résistance suffisante sinon un soutien passif est nécessaire car le bloc de la transmission est aussi rotatif. Son fonctionnement s'appuie sur l'équilibre des forces de rotation différentielle suivant des principes de géométrie dynamique.
À noter aussi que l'arbre de sortie tourne en sens inverse de celui de l'arbre d'entrée.
Le nom Diametroid est un acronyme de «diamétral et épicycloïde.
Figure 1
| Entrée (moteur) |
Diamètre 35 centimètres Longueur arbre/arbre 48 centimètres |
Sortie (roues) |
Aperçu du Diametroid
Le principal avantage du Diametroid réside dans les ratios de base de l'ordre de 50:1 pouvant être atteints avec les véhicules moteur à combustion interne. Il nécessite cependant l'adjonction d'un engrenage supplémentaire pour la marche arrière et le parking.
Le Diametroid n'a pas de référence statique et n'a aucune référence de vitesse externe fixe. Il ne voit que le différentiel de vitesses et de forces entre les arbres tournants. C'est pratiquement un convertisseur de couple avec une fonction d'embrayage intégrée. Il peut être adapté pour un rapport puissance/couple demandé ce qui convient à une large gamme de véhicules, qu'il s'agisse d'un vélo, d'une voiture, d'un moteur industriel, d'un camion ou d'engins de terrassement. La fonction intégrée d'embrayage est facilement adaptable pour bicycles à moteur où la marche arrière n'est généralement pas nécessaire.
L'efficacité évolutive pour toute demande de puissance de couple, la fonction d'embrayage intégrée, la capacité à maintenir le régime d'entrée constante, une gamme dynamique limitée que par la source d'alimentation et le dernier rapport de son entraînement de la chaîne de transmission associés, le fonctionnement silencieux, en font un organe de choix pour de nombreuses sources d'énergie de rotation.
| Page |
Composants du Diametroid
Le concept du Diametroid est basé sur une géométrie à deux dimensions. Les dessins utilisés pour expliquer les fonctions ne montrent pas des dents d'engrenage. Ils sont bien sûr nécessaires sur un modèle physique et sont expliqués plus loin. Sauf indication contraire, les diamètres des engrenages sont donnés pour les diamètres du cercle de base. Il met en œuvre 2 trains épicycloïdaux et un train hypocycloïdal.
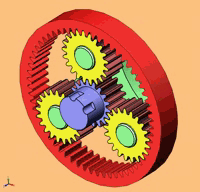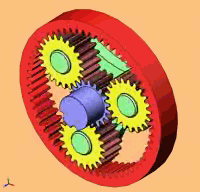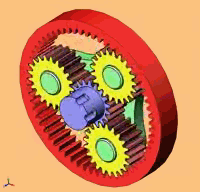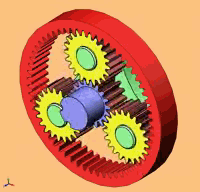
Je place ici l'éclaté du Diametroid de John Bisby pour en identifier en gros les composants :
La vue explosée montre la plupart des composants. Les roulements de soutient ne
sont pas montrés.
Rappel : l'intérêt d'un train épicycloïdal qui relie trois arbres de
transmission est de pouvoir déterminer
continument
la vitesse de rotation d'un
arbre en fonction de celle des deux autres.
On comprends alors que John Bisby ait eu l'idée de mettre deux trains épicycloïdaux en opposition, l'un meneur (le moteur) l'autre mené (les roues). Mais, que mettre entre les deux ?
| Page |
On comprends aussi que, pour mettre en présence des différentiels de forces, il ait eu recours à des pignons excentriques pour leurs porte-à-faux, ce qu'un engrenage à dentures ne permet pas puisqu'il met en présence un couple de forces.
Comment alors, avec des excentriques, relier la couronne du train en rouge aux pignons satellites en jaune ?
Au premier abord, ce Diametroid paraît bien compliqué. sur la figure_2 ce qui est normal car l'image représente l'ensemble mécanique à construire avec une logique d'assemblage, John Bisby en ayant déposé le brevet.
Il proposa donc la solution ci-dessous pour le train épicycloïde d'entrée (côté moteur) que j'ai schématisée avec FreeCAD :
Les engrenages des deux satellites A (gris-vert) n'attaquent pas la couronne comme normalement mais sont solidaires des deux excentriques B (violet) qui s'emboitent dans les évidements D d'une flasque (vert) et dont les broches C (violet) s'emboitent à leur tour dans les évidements E de la couronne (marron).
Tout naturellement, le train épicycloïdal de sortie reste pratiquement identique, à une différence près cependant : il comporte trois satellites au lieu de deux, vraisemblablement pour des raisons d'efforts plus importants du côté des roues.
J'ai donc continué à modéliser cette transmission ce qui est un bon exercice à la pratique de FreeCAD en se limitant au strict nécessaire. Ainsi les évidements d'allègement de poids n'ont pas été reconduits pour faciliter l'analyse et la compréhension.
Une première question indispensable dont on n'a pas la réponse, à première vue, sur l'éclaté de la figure_2 : quelles sont les pièces solidaires entre elles dans cette mécanique centrale d'auto-adaptation ?
| Page |
Au final, la figure 3 ci-dessous du Diametroid permet d'y voir un peu plus clair; Les cloisons de soutien n'ont pas été dessinées :
C'est donc bien ce train hypocycloïdal d'auto-adaptation dont il s'agit de découvrir le secret de fonctionnement... pour moi bien sûr !...:
À confirmer par la suite, il semblerait que les pièces 4, 7, 8 et 9 sont solidaires et boulonnées entre elles ?...
L'étage d'entrée utilise un engrenage planétaire (1) engrené dans deux engrenages satellites (2) solidaires à deux excentriques (3) qui tournent dans les évidements de la flasque-support (4) et dont les deux broches (3) s'emboitent dans les deux évidements (E sur la figure 3) de la partie (5) de la couronne. Ces deux excentriques (3) sont maintenus par le support (4) solidaire de l'engrenage de mise en phase (7) qui s'engrène dans l'engrenage de la partie (6) de la couronne. Donc, par rapport à la couronne (5-6), chaque dent de l'engrenage de mise en phase (7) décrit une orbite hypocycloïdale (voir figure 6 pour la configuration de base). L'assemblage de l'engrenage de mise en phase (7) et de la couronne (5-6) est configuré pour lui permettre de tourner autour de son propre axe et l'orbite hypocycloïdale autour de l'axe commun de référence.
l'étage de sortie utilise une engrenage planétaire (13) engrené dans deux ou plusieurs engrenages (12)satellites solidaires à des excentriques (12) qui tournent dans les évidements de la flasque-support (11) et dont les broches s'emboitent dans les évidements de la couronne (10). Comme pour l'étage d'entrée, le montage de l'hypocycloïdal ensemble de support et une orbite traduit hypocycloïdale. la sortie hypocycloïdes montage est configuré pour permettre de tourner autour de son propre centre et orbite autour de l'axe commun. les orbites hypocycloïdes de phases d'entrée et de sortie sont convertis en un (séparée] rotation de l'axe commun et reliés au support de phase opposée formation une connexion diamétrale.
Tous les pignons sont supportés par des roulements à rouleaux. les hypocycloïdes sont reliés aux engrenages planétaires au moyen de broches excentriques qui sont situées de manière rotative dans des paliers à aiguilles. Hypocycloïdale montage et la traduction de l'orbite est par paliers minces section à billes et à aiguilles.
Le principe de base du Diametroid implique une division de la force de rotation des arbres d'entrée et de sortie dans une transmission à différentiel et reliant les étages différentiels opposés dans un diamétrale - Format coaxial.
Une connexion diamétrale est fait plausible par l'inclusion d'un engrenage de mise en phase (7) sur l'étage d'entrée.
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
| Page |
--ooOoo-